
【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
【答案】(1)![]() ;(2)该公可若想获得10000万元的年利润,此设备的销售单价应是50万元.
;(2)该公可若想获得10000万元的年利润,此设备的销售单价应是50万元.
【解析】(1)根据点的坐标,利用待定系数法即可求出年销售量y与销售单价x的函数关系式;
(2)设此设备的销售单价为x万元/台,则每台设备的利润为(x﹣30)万元,销售数量为(﹣10x+1000)台,根据总利润=单台利润×销售数量,即可得出关于x的一元二次方程,解之取其小于70的值即可得出结论.
(1)设年销售量y与销售单价x的函数关系式为y=kx+b(k≠0),将(40,600)、(45,550)代入y=kx+b,得:
![]() ,
,
解得:![]() ,
,
∴年销售量y与销售单价x的函数关系式为y=﹣10x+1000.
(2)设此设备的销售单价为x万元/台,则每台设备的利润为(x﹣30)万元,销售数量为(﹣10x+1000)台,根据题意得:
(x﹣30)(﹣10x+1000)=10000,
整理,得:x2﹣130x+4000=0,
解得:x1=50,x2=80.
∵此设备的销售单价不得高于70万元,∴x=50.
答:该设备的销售单价应是50万元/台.


科目:初中数学 来源: 题型:
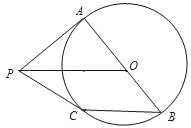
【题目】如图,AB是⊙O的直径,PA是⊙O的切线,点C在⊙O上,CB∥PO.
(1)判断PC与⊙O的位置关系,并说明理由;
(2)若AB=6,CB=4,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量![]() (升)关于加满油后已行驶的路程
(升)关于加满油后已行驶的路程![]() (千米)的函数图象.
(千米)的函数图象.

(1)根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;
(2)求![]() 关于
关于![]() 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数轴上有A 、B、C三个点,点A表示的数是-4,点B表示的数是-2,点C表示的数是2.
(1)在数轴上把A 、B、C三点表示出来,并比较各数的大小(用“<”连接);
(2)如何移动点B,使它到点A和点C的距离相等 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背最资料)
低碳生活的理念已逐步被人们所接受,据有关资料统计,一个人平均一年节约的用电相当于减排二氧化碳约18kg;一个人平均一年少买的衣服,相当于减排二氧化碳6kg.
(问题解决)
甲校对本校师生提出“节约用电”的倡议,乙校对本校师生提出“少买衣服”的倡议,2017年两校响应本校倡议的共有1000人,因此而减排二氧化碳总量约13200kg.问:2017年甲、乙两校响应倡议的人数分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】再读教材:
宽与长的比是 ![]() (约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.
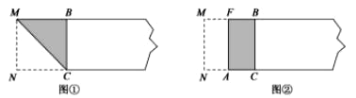
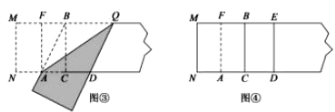
第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处,
第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形,
问题解决:
(1)图③中AB=________(保留根号);
(2)如图③,判断四边形 BADQ的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
(4)结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若一直重型运输卡车P沿道路ON方向行驶的速度为18千米/时.

(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店中销售水果时采用了三种组合搭配的方式进行销售,甲种搭配是:2千克A水果,4千克B水果;乙种搭配是:3千克A水果,8千克B水果,1千克C水果;丙种搭配是:2千克A水果,6千克B水果,1千克C水果;如果A水果每千克售价为2元,B水果每千克售价为1.2元,C水果每千克售价为10元,某天,商店采用三种组合搭配的方式进行销售后共得销售额441.2元,并且A水果销售额116元,那么C水果的销售额是______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,BC∥OA,∠B=∠A=108°,试解答下列问题:
(1)如图1所示,则∠O= °,并判断OB与AC平行吗?为什么?
(2)如图2,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于 °;
(3)在第(2)题的条件下,若平行移动AC,如图3.
①求∠OCB:∠OFB的值;
②当∠OEB=∠OCA时,求∠OCA的度数(直接写出答案,不必写出解答过程).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com