试题分析:(1)利用外角性质,求得∠BAM+∠ABN=270°;由AP平分∠MAB,BP平分∠ABN可得∠BAP+∠ABP的度数,再根据三角形内角和定理求解即可;
(2)与问题(1)的思路相同;
(3)利用外角性质,求得∠BAM+∠ABN=∠MON+∠ABO+∠MON+∠BAO=(∠MON+∠ABO+∠BAO)+∠MON=180°+∠MON;由AP平分∠MAB,BP平分∠ABN.求∠BAP+∠ABP,最后根据三角形内角和定理即可求得所求的度数.
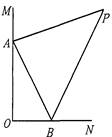
(1)∵∠BAM=∠AOB+∠ABO,∠ABN=∠AOB+∠BAO
∴∠BAM+∠ABN="∠AOB+∠ABO+∠AOB+∠BAO=180°+" 90°=270°
∵AP平分∠MAB,BP平分∠ABN
∴∠BAP=∠BAM,∠ABP=∠ABN
∴∠BAP+∠ABP=
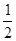
(∠BAM+∠ABN)=135°
在△ABP中,∠BAP+∠ABP+∠P=180°
∴∠P="180°-" 135°=45°;
(2)∵∠BAM=∠AOB+∠ABO,∠ABN=∠AOB+∠BAO
∴∠BAM+∠ABN="∠AOB+∠ABO+∠AOB+∠BAO=180°+" 80°=260°
∵AP平分∠MAB,BP平分∠ABN
∴∠BAP=∠BAM,∠ABP=∠ABN
∴∠BAP+∠ABP=
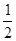
(∠BAM+∠ABN)=130°
在△ABP中,∠BAP+∠ABP+∠P=180°
∴∠P="180°-" 130°=50°;
(3)∠MON+2∠P=180°
∵∠BAM=∠MON+∠ABO,∠ABN=∠MON+∠BAO
∴∠BAM+∠ABN="∠MON+∠ABO+∠MON+∠BAO" ="180°+∠MON"
∵AP平分∠MAB,BP平分∠ABN
∴∠BAP=∠BAM,∠ABP=∠ABN
∴∠BAP+∠ABP=
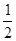
(∠BAM+∠ABN)=
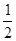
(180°+∠MON)
在△ABP中,∠BAP+∠ABP+∠P=180°,(180°+∠MON)+∠P=180°
∴∠MON+2∠P=180°.
点评:解题的关键是熟练掌握三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角的和.

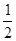 (∠BAM+∠ABN)=135°
(∠BAM+∠ABN)=135°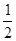 (∠BAM+∠ABN)=130°
(∠BAM+∠ABN)=130°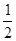 (∠BAM+∠ABN)=
(∠BAM+∠ABN)=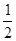 (180°+∠MON)
(180°+∠MON)

 名校课堂系列答案
名校课堂系列答案