
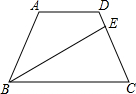
 如图,在等腰梯形ABCD中,AD∥BC,AD=1,BC=3,∠ABC的平分线交腰CD于点E(不与点C、D重合).
如图,在等腰梯形ABCD中,AD∥BC,AD=1,BC=3,∠ABC的平分线交腰CD于点E(不与点C、D重合).分析 (1)延长BA、CD交于点F,构造等腰△BCF,由于AD∥BC,所以△ADF∽△BCF,利用对应边的比相等即可求出AF=1,所以可知△ADF是等边三角形,从而可知△FBE是直角三角形,利用勾股定理即可求出BE;
(2)延长AD,BE交于点F,利用角平分线构造等腰三角形△ABF,然后证明△DEF∽△CBE,利用对应边的比相等即可求出y与x的关系式;
(3)若△ABE是直角三角形,由于题目没有说明哪一个是直角,所以要分三种情况讨论:①当∠BAE=90°;②当∠AEB=90°;③当∠ABE=90°.
解答 解: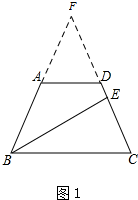 (1)如图1,延长BA、CD交于点F,
(1)如图1,延长BA、CD交于点F,
∵四边形ABCD是等腰梯形,
∴∠ABC=∠DCB,
∵AD∥BC,
∴∠FAD=∠FDA,
∴△FAD是等腰三角形,
∵AD∥BC,
∴△ADF∽△BCF,
∴$\frac{AD}{BC}$=$\frac{AF}{BC}$
∵AB=2,AD=1,BC=3,
∴AF=1,
∴△FDA是等边三角形,
∴∠FAD=60°
∵BE平分∠ABC,
∴∠FBE=30°,
∴∠FEB=90°,
∵BF=3,
∴FE=$\frac{3}{2}$
∴由勾股定理可知:BE=$\frac{3}{2}\sqrt{3}$;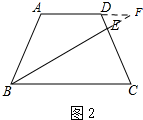 (2)如图2,延长AD,BE交于点F,
(2)如图2,延长AD,BE交于点F,
∵AF∥BC,
∴∠AFB=∠FBC,
∵BE平分∠ABC,
∴∠ABF=∠FBC,
∴∠AFB=∠ABF,
∴AB=AF,
∵四边形ABCD是等腰梯形,
∴AB=CD=CE+ED=x+y,
∴AF=x+y,
∴DF=AF-AD=x+y-1,
∵DF∥BC,
∴△DEF∽△CBE,
∴$\frac{DF}{BC}$=$\frac{DE}{CE}$,
∴$\frac{x+y-1}{3}$=$\frac{y}{x}$,
∴y=$\frac{{x}^{2}-x}{3-x}$(1<x<3);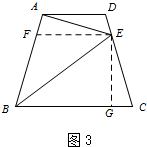 (3)如图3,当∠BAE=90°时,
(3)如图3,当∠BAE=90°时,
过点E作EF∥BC交AB于点F,
过点E作EG⊥BC于点G,
∴AF=DE=y,BF=CE=x,∠FEB=∠EBC,
∵BE平分∠ABC,
∴AE=EG,∠ABE=∠EBC,AB=BG
∴∠ABE=∠FEB,
∴BF=FE,
∴CE=FE,
在Rt△AEF与Rt△GEC中,
$\left\{\begin{array}{l}{FE=CE}\\{AE=EG}\end{array}\right.$,
∴Rt△AEF≌Rt△GEC(HL),
∴AF=GC=y,
∵BC=BG+GC,
∴3=x+y+y,
∵y=$\frac{{x}^{2}-x}{3-x}$,
∴解得:x=-2$±\sqrt{13}$,
∵1<x<3,
∴x=$\sqrt{13}$-2,
∴y=$\frac{5-\sqrt{13}}{2}$,
∴AB=x+y=$\frac{\sqrt{13}+1}{2}$,
如图4,当∠AEB=90°时,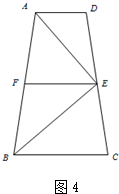 过点E作EF∥BC交AB于点F,
过点E作EF∥BC交AB于点F,
∴AF=DE=y,BF=CE=x,∠FEB=∠EBC
∵BE平分∠ABC,
∴∠FBE=∠EBC,
∴∠FBE=∠FEB,
∴BF=EF=x,
∵∠FAE=90°-∠FBE
∠AEF=90°-∠FEB,
∴∠FAE=∠AEF,
∴AF=EF,
∴y=x,
∵y=$\frac{{x}^{2}-x}{3-x}$,
∴解得:x=2或x=0
∵1<x<3,
∴x=2,
∴AB=x+y=2x=4,
当∠ABE=90°时,
∵BE平分∠ABC,
∴∠ABE=∠CBE=90°,
此情况不存在,
综上所述,当△ABE为直角三角形时,腰AB的长为$\frac{\sqrt{13}+1}{2}$或2.
点评 本题考查等腰梯形的综合问题,涉及等腰梯形的性质,梯形常用辅助线作法,全等三角形的判定和性质,相似三角形的判定和性质,解方程等知识内容,综合程度较高,需要学生将各章内容熟练运用.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{19}{2}$ | B. | $\frac{21}{2}$ | C. | 7 | D. | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
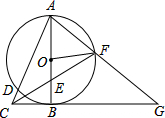 如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在$\widehat{AB}$的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在$\widehat{AB}$的中点,连接AF并延长与CB的延长线相交于点G,连接OF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com