
分析 (1)首先根据题意画出树状图,由树状图求得所有等可能的结果与小明获胜的情况,继而利用概率公式即可求得答案;
(2)首先根据题意画出树状图,由树状图求得所有等可能的结果与小明、小强获胜的情况,继而利用概率公式求得其概率,比较概率,则可得到他们制定的游戏规则是否公平,注意此题属于放回实验.
解答 解:(1)根据题意列树形图如下: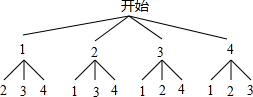
∵共有12种等可能的结果,小明获胜的有(2,1),(3,1),(3,2),(4,1),(4,2),(4,3)共6种情况,
∴小明获胜的概率为$\frac{6}{12}$=$\frac{1}{2}$;
(2)画树状图得: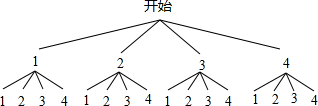
∵共有16种等可能的结果,其中符合x>y的有6种,
共有16种等可能的结果,∴P小明=$\frac{6}{16}$=$\frac{3}{8}$,P小强=$\frac{10}{16}$=$\frac{5}{8}$,
∵$\frac{3}{8}$≠$\frac{5}{8}$,
∴不公平.
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平;用到的知识点为:概率=所求情况数与总情况数之比.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
| 甲种图书 | 乙种图书 | |
| 进价(元/本) | 16 | 28 |
| 售价(元/本) | 26 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
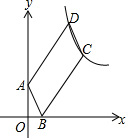 如图,在直角坐标系中,平行四边形ABCD的顶点A(0,2)、B(1,0)在x轴、y轴上,另两个顶点C、D在第一象限内,且AD=3AB.若反比例函数$y=\frac{k}{x}$(k>0)的图象经过C,D两点,则k的值是24.
如图,在直角坐标系中,平行四边形ABCD的顶点A(0,2)、B(1,0)在x轴、y轴上,另两个顶点C、D在第一象限内,且AD=3AB.若反比例函数$y=\frac{k}{x}$(k>0)的图象经过C,D两点,则k的值是24.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
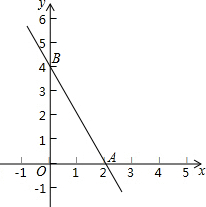 如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.
如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知一块圆心角为270°的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是( )
如图,已知一块圆心角为270°的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是( )| A. | 40cm | B. | 50cm | C. | 60cm | D. | 80cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com