练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下图，已知直线y＝4－x与反比例函数y＝(m＞0，x＞0)的图象交于A、B两点，与x轴、y轴分别相交于C、D两点．

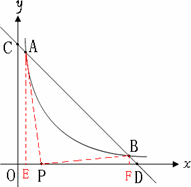
    (1)如果点A的横坐标为1，利用函数图象求关于x的不等式4－x＜的解集；

    (2)是否存在以AB为直径的圆经过点P(1，0)？若存在，求出m的值；若不存在，请说明理由．

    答案：
    解析：

    　　解：(1)∴点A的横坐标为1，点A在直线

    　　y＝4－x的图象上，y＝4－1＝3，

    　　∴点A的坐标为(1，3)，

    　　点A在反比例函数y＝(m＞0，x＞0)的图象的

    　　图象上，m＝xy＝3，

    　　∵点A、B是直线y＝4－x与反比例函数

    　　y＝(x＞0)的图象的交点，∴4－x＝，

    　　解得x＝1或x＝3，点B的横坐标为3，∴4－x＜的解集为x＜1或x＞3．

    　　

    　　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：非常讲解·教材全解全析　数学　七年级下　（配北师大课标） 北师大课标 题型：047

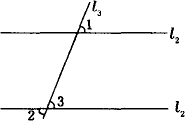
    如下图，已知直线l1和l2分别与直线l3相交，∠1＝∠3，求证：∠1＝∠2．

    查看答案和解析>>

    科目：初中数学 来源：2013年四川省乐山市高级中等学校招生考试数学 题型：013

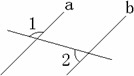
    下图，已知直线a∥b，∠1＝131°，则∠2等于

    [　　]

    A．39°

    B．41°

    C．49°

    D．59°

    查看答案和解析>>

    科目：初中数学 来源：2013年重庆市高级中等学校招生考试数学B卷 题型：044

    下图，已知抛物线y＝x2＋bx＋c的图像与x轴的一个交点为B(5，0)，另一个交点为A，且与y轴交于点C(0，5)．

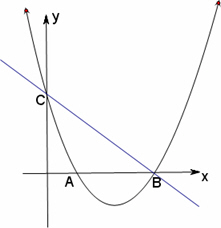
    (1)求直线BC与抛物线的解析式；

    (2)若点M是抛物线在x轴下方图像上的一动点，过点M作MN∥y轴交直线BC于点N，求MN的最大值；

    (3)在(2)的条件下，MN取得最大值时，若点P是抛物线在x轴下方图像上任意一点，以BC为边作平行四边形CBPQ，设平行四边形CBPQ的面积为S1，△ABN的面积为S2，且S1＝6S2，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源：2009年山西省中考数学试题 题型：044

    如下图，已知直线l1∶y＝与直线l2∶y＝－2x＋16相交于点C，l1、l2分别交x轴于A、B两点．矩形DEFG的顶点D、E分别在直线l1、l2上，顶点F、G都在x轴上，且点G与点B重合．

    (1)求△ABC的面积；

    (2)求矩形DEFG的边DE与EF长；

    (3)若矩形DEFG从原点出发，沿x轴的反方向以每秒1个单位长度的速度平移，设移动时间为t(0≤t≤12)秒，矩形DEFG与△ABC重叠部分的面积为S，求S关于t的函数关系式，并写出相应的t的取值范围．

    查看答案和解析>>

    同步练习册答案