
 支援C粮仓,从B粮仓运出该粮仓存粮的
支援C粮仓,从B粮仓运出该粮仓存粮的 支援C粮仓,这时A,B两处粮仓的
支援C粮仓,这时A,B两处粮仓的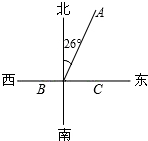 存粮吨数相等.(sin26°=0.44,cos26°=0.90,tan26°=0.49)
存粮吨数相等.(sin26°=0.44,cos26°=0.90,tan26°=0.49)
 ×270=162(吨),
×270=162(吨), ×180=72(吨),
×180=72(吨),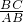 ,
,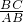 ,要求BC的长,可以运用三角函数解直角三角形.
,要求BC的长,可以运用三角函数解直角三角形.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
 C1绕点A1逆时针旋转180°,得到△A1B2C2.
C1绕点A1逆时针旋转180°,得到△A1B2C2.查看答案和解析>>
科目:初中数学 来源: 题型:
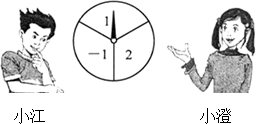 (2013•澄江县一模)如图,一转盘被等分成三个扇形,上面分别标有-1,1,2中的一个数,指针位置固定,转动转盘后任其自由停止,这时,某个扇形会恰好停在指针所指的位置,并相应得到这个扇形上的数(若指针恰好指在等分线上,当做指向右边的扇形).
(2013•澄江县一模)如图,一转盘被等分成三个扇形,上面分别标有-1,1,2中的一个数,指针位置固定,转动转盘后任其自由停止,这时,某个扇形会恰好停在指针所指的位置,并相应得到这个扇形上的数(若指针恰好指在等分线上,当做指向右边的扇形).查看答案和解析>>
科目:初中数学 来源: 题型:
 余的一半作为绿化用地.
余的一半作为绿化用地.查看答案和解析>>
科目:初中数学 来源: 题型:
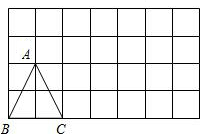
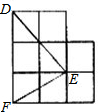 如图,方格纸中△DEF的三个顶点分别在小正方形的顶点上,像这样的三个顶点都在格点上的三角形叫格点三角形,则图中这样的格点三角形有( )个与△DEF全等.
如图,方格纸中△DEF的三个顶点分别在小正方形的顶点上,像这样的三个顶点都在格点上的三角形叫格点三角形,则图中这样的格点三角形有( )个与△DEF全等.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com