
|
|
|
| 1 |
| (a-b)2 |
| 1 |
| (b-c)2 |
| 1 |
| (c-a)2 |
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| c-a |
|
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| c-a |
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| c-a |
|
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| c-a |
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| c-a |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过380元 | 不优惠 |
| 超过380元,但不超过500元 | 售价打九折 |
| 超过500元 | 售价打八折 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1:直线y= kx+4k(k≠0)交x轴于点A,交y轴于点C,点M(2,m)为直线AC上一点,过点M的直线BD交x轴于点B,交y轴于点D.
(1)求的值(用含有k的式子表示.);
(2)若SBOM =3S
DOM,且k为方程(k+7)(k+5)-(k+6)(k+5=
的根,求直线BD的解析式.
(3)如图2,在(2)的条件下,P为线段OD之间的动点(点P不与点O和点D重合),OE
上AP于E,,DF上AP于F,下列两个结论:①值不变;②
值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值,
查看答案和解析>>
科目:初中数学 来源: 题型:

 的值(用含有k的式子表示.);
的值(用含有k的式子表示.); BOM =3S
BOM =3S DOM,且k为方程(k+7)(k+5)-(k+6)(k+5=
DOM,且k为方程(k+7)(k+5)-(k+6)(k+5= 的根,求直线BD的解析式.
的根,求直线BD的解析式. 值不变;②
值不变;② 值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值,
值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值,查看答案和解析>>
科目:初中数学 来源:2011届北京市门头沟区初三第一学期期末数学卷 题型:解答题
如图1:直线y= kx+4k(k≠0)交x轴于点A,交y轴于点C,点M(2,m)为直线AC上一点,过点M的直线BD交x轴于点B,交y轴于点D.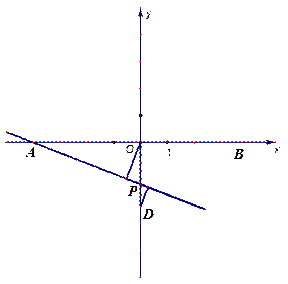
(1)求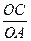 的值(用含有k的式子表示.);
的值(用含有k的式子表示.);
(2)若S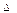 BOM =3S
BOM =3S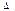 DOM,且k为方程(k+7)(k+5)-(k+6)(k+5=
DOM,且k为方程(k+7)(k+5)-(k+6)(k+5= 的根,求直线BD的解析式.
的根,求直线BD的解析式.
(3)如图2,在(2)的条件下,P为线段OD之间的动点(点P不与点O和点D重合),OE
上AP于E,,DF上AP于F,下列两个结论:①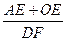 值不变;②
值不变;②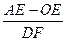 值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值,
值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值,
查看答案和解析>>
科目:初中数学 来源:2010-2011学年北京市门头沟区初三第一学期期末数学卷 题型:解答题
如图1:直线y= kx+4k(k≠0)交x轴于点A,交y轴于点C,点M(2,m)为直线AC上一点,过点M的直线BD交x轴于点B,交y轴于点D.
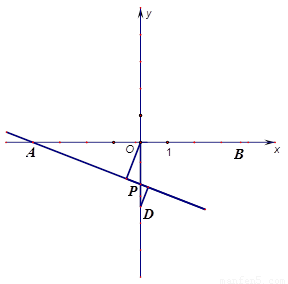
(1)求 的值(用含有k的式子表示.);
的值(用含有k的式子表示.);
(2)若S BOM =3S
BOM =3S DOM,且k为方程(k+7)(k+5)-(k+6)(k+5=
DOM,且k为方程(k+7)(k+5)-(k+6)(k+5= 的根,求直线BD的解析式.
的根,求直线BD的解析式.
(3)如图2,在(2)的条件下,P为线段OD之间的动点(点P不与点O和点D重合),OE
上AP于E,,DF上AP于F,下列两个结论:① 值不变;②
值不变;②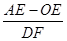 值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值,
值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com