
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③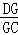 =
=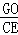 ;④(a﹣b)2•S△EFO=b2•S△DGO.其中结论正确的个数是( )
;④(a﹣b)2•S△EFO=b2•S△DGO.其中结论正确的个数是( )

A. 4个 B.3个 C.2个 D. 1个
B 证明:①∵四边形ABCD和四边形CEFG是正方形,
∴BC=DC,CG=CE,∠BCD=∠ECG=90°,
∴∠BCG=∠DCE,
在△BCG和△DCE中,
 ,
,
∴△BCG≌△DCE(SAS),
故①正确;
②延长BG交DE于点H,
∵△BCG≌△DCE,
∴∠CBG=∠CDE,
又∵∠CBG+∠BGC=90°,
∴∠CDE+∠DGH=90°,
∴∠DHG=90°,
∴BH⊥DE;
∴BG⊥DE.
故②正确;
③∵四边形GCEF是正方形,
∴GF∥CE,
∴ =
=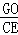 ,
,
∴ =
= 是错误的.
是错误的.
故③错误;
④∵DC∥EF,
∴∠GDO=∠OEF,
∵∠GOD=∠FOE,
∴△OGD∽△OFE,
∴ =(
=( )2=(
)2=( )2=
)2= ,
,
∴(a﹣b)2•S△EFO=b2•S△DGO.
故④正确;
.


科目:初中数学 来源: 题型:
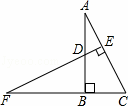
如图,在Rt△ABC中,∠ABC=90°,点D在边AB上,使DB=BC,过点D作EF⊥AC,分别交AC于点E,CB的延长线于点F.
求证:AB=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.
(1)若AE=CF;
①求证:AF=BE,并求∠APB的度数;
②若AE=2,试求AP•AF的值;
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
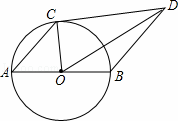
如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切,BD∥AC.
(1)图中∠OCD= °,理由是 ;
(2)⊙O的半径为3,AC=4,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com