
 cm.若把△ADC的顶点C沿CB所在射线滑动,顶点A始终不离开AC,如图②所示,当点D运动到与C点重合时,即停止运动,如图③所示.
cm.若把△ADC的顶点C沿CB所在射线滑动,顶点A始终不离开AC,如图②所示,当点D运动到与C点重合时,即停止运动,如图③所示.
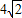 cm,∴AC=8cm;(4分)
cm,∴AC=8cm;(4分) )cm.(5分)
)cm.(5分) cm;
cm; )cm.(12分)
)cm.(12分)

科目:初中数学 来源:2010年浙江省杭州市萧山区中考数学模拟试卷(新湾初中 张坚勇)(解析版) 题型:选择题
 的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为( )
的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为( )
查看答案和解析>>
科目:初中数学 来源:2010年江苏省南通市崇川区中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年江苏省南通市崇川区中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年江苏省南通市崇川区中考数学模拟试卷(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2010年江苏省南通市崇川区中考数学模拟试卷(解析版) 题型:选择题
 的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为( )
的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com