
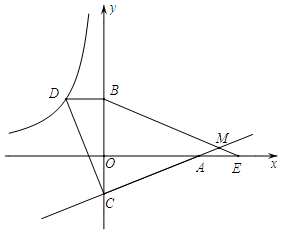
 ��ͼ����֪��D�ڷ���������y=$\frac{m}{x}$��ͼ���ϣ�����D��x���ƽ���߽�y���ڵ�B��0��3��������A��5��0����ֱ��y=kx+b��y���ڵ�C����BD=OC��tan��OAC=$\frac{2}{5}$��
��ͼ����֪��D�ڷ���������y=$\frac{m}{x}$��ͼ���ϣ�����D��x���ƽ���߽�y���ڵ�B��0��3��������A��5��0����ֱ��y=kx+b��y���ڵ�C����BD=OC��tan��OAC=$\frac{2}{5}$������ ��1����A����������OA�ij������������Ǻ����Ķ�������OC�ij��������C��D�����꣬�����ô���ϵ���������ֱ��AC�Ľ���ʽ��
��2����������֤����OAC�ա�BCD�����ɽǵĺͲ����á�OAC+��BCA=90�㣬��֤��AC��CD��
��3������AD����֤���ı���AEBDΪƽ���ı��Σ��ɵó���ACDΪ����ֱ�������Σ������ô𰸣�
��� �⣺
��1����A��5��0����
��OA=5��
��tan��OAC=$\frac{2}{5}$��
��$\frac{OC}{OA}$=$\frac{2}{5}$�����OC=2��
��C��0��-2����
��BD=OC=2��
��B��0��3����BD��x�ᣬ
��D��-2��3����
��m=-2��3=-6��
��y=-$\frac{6}{x}$��
��ֱ��AC��ϵʽΪy=kx+b��
�߹�A��5��0����C��0��-2����
��$\left\{\begin{array}{l}{0=5k+b}\\{-2=b}\end{array}\right.$�����$\left\{\begin{array}{l}{k=\frac{2}{5}}\\{b=-2}\end{array}\right.$��
��y=$\frac{2}{5}$x-2��
��2����B��0��3����C��0��-2����
��BC=5=OA��
�ڡ�OAC�͡�BCD��
$\left\{\begin{array}{l}{OA=BC}\\{��AOC=��DBC}\\{OC=BD}\end{array}\right.$
���OAC�ա�BCD��SAS����
��AC=CD��
���OAC=��BCD��
���BCD+��BCA=��OAC+��BCA=90�㣬
��AC��CD��
��3����BMC=45�㣮
��ͼ������AD��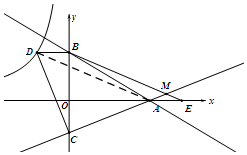
��AE=OC��BD=OC��AE=BD��
��BD��x�ᣬ
���ı���AEBDΪƽ���ı��Σ�
��AD��BM��
���BMC=��DAC��
�ߡ�OAC�ա�BCD��
��AC=CD��
��AC��CD��
���ACDΪ����ֱ�������Σ�
���BMC=��DAC=45�㣮
���� ����Ϊ�������������ۺ�Ӧ�ã��漰����ϵ������ȫ�������ε��ж������ʡ�ƽ���ı��ε��ж������ʡ�����ֱ�������ε��ж������ʵ�֪ʶ���ڣ�1�������C��D�������ǽ���Ĺؼ����ڣ�2����֤�á�OAC�ա�BCD�ǽ���Ĺؼ����ڣ�3����֤���ı���AEBDΪƽ���ı����ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 628ml | B�� | 603ml | C�� | 588ml | D�� | 568ml |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y��0��y��x���������С | B�� | y��0��y��x����������� | ||
| C�� | y��0��y��x���������С | D�� | y��0��y��x����������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x•��-xy��2=-2x3y | B�� | ��-x2��3�£�-x3��2=1 | ||
| C�� | ��$\frac{3}{4}$a3-$\frac{1}{2}$b��•2ab=$\frac{3}{2}$a4b-ab2 | D�� | ��3m-1��2=9m2-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 �ҹ��Ŵ���ѧ�����á�IJ�Ϸ��ǡ��ҵ�����������ļ��㷽������IJ�Ϸ��ǡ���������Բ���ֱ���ݺ���������Ƕ��һ��������ʱ��Բ�����������γɵļ����壬��ͼ��ʾ�ļ������ǿ����γɡ�IJ�Ϸ��ǡ���һ��ģ�ͣ���������ͼ�ǣ�������
�ҹ��Ŵ���ѧ�����á�IJ�Ϸ��ǡ��ҵ�����������ļ��㷽������IJ�Ϸ��ǡ���������Բ���ֱ���ݺ���������Ƕ��һ��������ʱ��Բ�����������γɵļ����壬��ͼ��ʾ�ļ������ǿ����γɡ�IJ�Ϸ��ǡ���һ��ģ�ͣ���������ͼ�ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
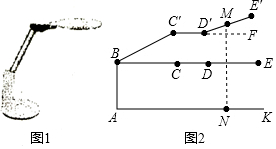 �г���һ��۵ƣ���ͼ1��������Բ�����Դ��������������ת֧�ܵȵĿ��ȣ��õ����IJ���ṹͼ����ͼ2��������AB������AK����ת֧��BC���Ƶ�B��ת��ת��ͷCD������AK��Բ�����Դ����ת֧������ƽ������Ƶ�D��ת����ֱ��DEΪ20cm������ת֧����ת��BC�䴦��Բ�����ԴDE��ת��D��E�䴦����ʱԲ�����Դ����M������ľ���MN=40cm����֪AB=20cm����CBC=37�㣬��E��D��F=24�㣬����ת֧��BC��Ϊ��������cm�������ȷ��1cm���ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��sin24���0.40��cos24���0.91��tan24���0.45��
�г���һ��۵ƣ���ͼ1��������Բ�����Դ��������������ת֧�ܵȵĿ��ȣ��õ����IJ���ṹͼ����ͼ2��������AB������AK����ת֧��BC���Ƶ�B��ת��ת��ͷCD������AK��Բ�����Դ����ת֧������ƽ������Ƶ�D��ת����ֱ��DEΪ20cm������ת֧����ת��BC�䴦��Բ�����ԴDE��ת��D��E�䴦����ʱԲ�����Դ����M������ľ���MN=40cm����֪AB=20cm����CBC=37�㣬��E��D��F=24�㣬����ת֧��BC��Ϊ��������cm�������ȷ��1cm���ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��sin24���0.40��cos24���0.91��tan24���0.45��| A�� | 18 | B�� | 20 | C�� | 25 | D�� | 27 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com