

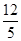 ;(2)t=1.2s,S△EGR =
;(2)t=1.2s,S△EGR =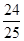 ;(3)
;(3) ;(4)
;(4)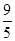 或4.2或5.7
或4.2或5.7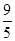 ,BQ=
,BQ=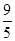 +t,先根据QR∥BA证得△RQC∽△ABC,再根据相似对角线的性质即得结果;
+t,先根据QR∥BA证得△RQC∽△ABC,再根据相似对角线的性质即得结果;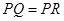 、
、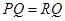 、当
、当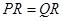 三种情况,根据锐角三角函数的定义及等腰三角形的性质求解即可.
三种情况,根据锐角三角函数的定义及等腰三角形的性质求解即可.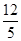 ;(2)t=1.2s,S△EGR =
;(2)t=1.2s,S△EGR =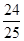 ;
;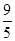 ,BQ=
,BQ=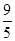 +t,
+t,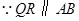 ,
,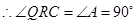 .
.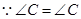 ,
, ,
,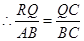 ,
,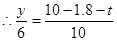 ,
, ;
;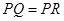 时,过点
时,过点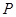 作
作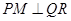 于
于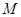 ,则
,则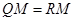 .
.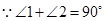 ,
, ,
,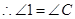 .
.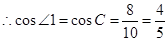 ,
,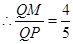 ,
,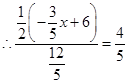 ,
,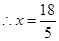 .此时t=
.此时t=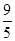 .
.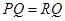 时,
时,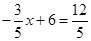 ,
,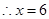 .此时t=4.2.
.此时t=4.2.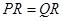 时,则
时,则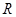 为
为 中垂线上的点,于是点
中垂线上的点,于是点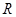 为
为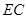 的中点,
的中点,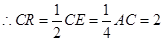 .
.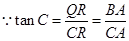 ,
,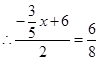 ,
,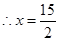 .此时t=5.7.
.此时t=5.7.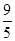 或4.2或5.7时,
或4.2或5.7时,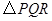 为等腰三角形.
为等腰三角形.

 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源:不详 题型:填空题
 平移得到抛物线m,抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线
平移得到抛物线m,抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线 交于点Q,则图中阴影部分的面积为___________.
交于点Q,则图中阴影部分的面积为___________.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,
,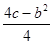 ),AB=|x1-x2|,若S△APB=1,则b与c的关系式是( ).
),AB=|x1-x2|,若S△APB=1,则b与c的关系式是( ). | A.b2-4c+1=0 | B.b2-4c-1=0 | C.b2-4c+4=0 | D.b2-4c-4=0 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 沿x轴翻折,得到抛物线c2,如图所示.
沿x轴翻折,得到抛物线c2,如图所示.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com