
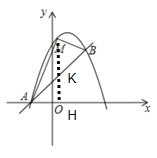
【题目】如图,已知直线AB与抛物线C:y=ax2+2x+c相交于点A(﹣1,0)和点B(2,3)两点.
(1)求抛物线C函数表达式;
(2)若点M是位于直线AB上方抛物线上的一动点,当![]() 的面积最大时,求此时
的面积最大时,求此时![]() 的面积S及点M的坐标.
的面积S及点M的坐标.

【答案】(1) y=﹣x2+2x+3;(2) △MAB的面积最大值是![]() ,M(
,M(![]() ,
,![]() )
)
【解析】
(1)利用待定系数法求出抛物线的解析式即可;
(2)过点M作MH⊥x轴于H,交直线AB于K,利用待定系数法可得yAB=x+1,设点M(x,﹣x2+2x+3),则K(x,x+1),可得S△MAB=![]() ,即可求出
,即可求出![]() 的最大面积S及点M的坐标.
的最大面积S及点M的坐标.
(1)由题意把点(﹣1,0)、(2,3)代入y=ax2+2x+c,
得![]() ,解得
,解得![]() ,
,
∴此抛物线C函数表达式为:y=﹣x2+2x+3;
(2)如图,过点M作MH⊥x轴于H,交直线AB于K,
将点(﹣1,0)、(2,3)代入y=kx+b中,
得![]() ,解得
,解得![]() ,
,
∴yAB=x+1,
设点M(x,﹣x2+2x+3),则K(x,x+1),则MK=﹣x2+2x+3﹣(x+1)=﹣x2+x+2,
∴S△MAB
=S△AMK+S△BMK
=![]() MK(xM﹣xA)+
MK(xM﹣xA)+ ![]() MK(xB﹣xM)
MK(xB﹣xM)
=![]() MK(xB﹣xA)
MK(xB﹣xA)
=![]() ×(-x2+x+2)×3
×(-x2+x+2)×3
=![]() ,
,
∵![]() ,当x=
,当x=![]() 时,S△MAB最大=
时,S△MAB最大=![]() ,此时
,此时![]() ,
,
∴△MAB的面积最大值是![]() ,M(
,M(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】网络销售是一种重要的销售方式.某乡镇农贸公司新开设了一家网店,销售当地农产品.其中一种当地特产在网上试销售,其成本为每千克10元.公司在试销售期间,调查发现,每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中![]() ).
).
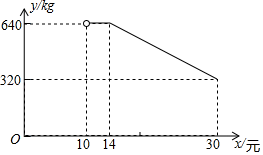
(1)直接写出y与x之间的函数关系式及自变量的取值范围.
(2)若农贸公司每天销售该特产的利润要达到3100元,则销售单价x应定为多少元?
(3)设每天销售该特产的利润为W元,若![]() ,求:销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
,求:销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为_____.
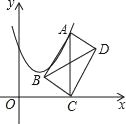
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线 y=ax2 -2ax+4(a<0) 交 x 轴于点 A、B,与 y 轴交于点 C,AB=6.
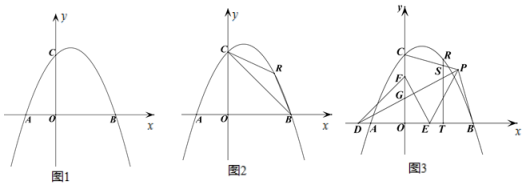
(1)如图 1,求抛物线的解析式;
(2) 如图 2,点 R 为第一象限的抛物线上一点,分别连接 RB、RC,设△RBC 的面积为 s,点 R 的横坐标为 t,求 s 与 t 的函数关系式;
(3)在(2)的条件下,如图 3,点 D 在 x 轴的负半轴上,点 F 在 y 轴的正半轴上,点 E 为 OB 上一点,点 P 为第一象限内一点,连接 PD、EF,PD 交 OC 于点 G,DG=EF,PD⊥EF,连接 PE,∠PEF=2∠PDE,连接 PB、PC,过点R 作 RT⊥OB 于点 T,交 PC 于点 S,若点 P 在 BT 的垂直平分线上,OB-TS=![]() ,求点 R 的坐标.
,求点 R 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与x轴、y轴分别交于点B、C;抛物线y=﹣x2+bx+c经过B、C两点,并与x轴交于另一点A.
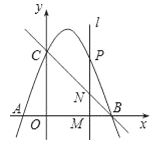
(1)求该抛物线所对应的函数关系式;
(2)设P(x,y)是(1)所得抛物线上的一个动点,过点P作直线l⊥x轴于点M,交直线BC于点N.
①若点P在第一象限内.试问:线段PN的长度是否存在最大值?若存在,求出它的最大值及此时x的值;若不存在,请说明理由;
②求以BC为底边的等腰△BPC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=x2﹣4x+3
(1)求其图象与x轴交点A、B的坐标(A在B左边);
(2)在坐标系中画出函数图象;
(3)若函数图形的顶点为C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,直径DE⊥AB于点F,交BC于点 M,DE的延长线与AC的延长线交于点N,连接AM.
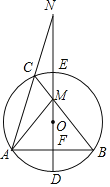
(1)求证:AM=BM;
(2)若AM⊥BM,DE=8,∠N=15°,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以点M(0, ![]() )为圆心,以
)为圆心,以![]() 长为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于P点,连接PC交x轴于E.
长为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于P点,连接PC交x轴于E.
(1)求出CP所在直线的解析式;
(2)连接AC,请求△ACP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
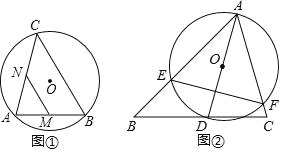
【题目】(I)圆中最长的弦是________;
(Ⅱ)如图①,AB 是⊙O 的弦,AB=8,点 C 是⊙O 上的一个动点,且∠ACB=45°, 若点 M、N 分别是 AB、AC 的中点,则 MN 长度的最大值是___;
(Ⅲ)如图②,△ABC 中,∠BAC=60°,∠ABC=45°,AB=4,D 是边 BC 上的一个动点,以 AD 为直径画⊙O,分别交 AB、AC 于点 E、F,连接 EF,则线段 EF 长度的最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com