

分析 (1)待定系数法求解可得;
(2)先根据题意表示出翻折后抛物线解析式,再求出y=1时x的值,继而可分-2≤x≤2、-2$\sqrt{2}$≤x<-2或2$<x≤2\sqrt{2}$、x<-2$\sqrt{2}$或x>2$\sqrt{2}$三种情况,根据两点间距离公式列式表示出PO与PD的差即可得出答案.
解答 解:(1)根据题意设抛物线解析式为y=ax2-1,
将点A(-2,0)代入,得:4a-1=0,
解得:a=$\frac{1}{4}$,
∴抛物线的解析式为y=$\frac{1}{4}$x2-1;
(2)如图,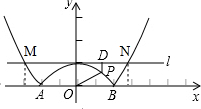
根据题意,当-2≤x≤2时,y=-$\frac{1}{4}$x2+1;
当x<-2或x>2时,y=$\frac{1}{4}$x2-1;
由$\left\{\begin{array}{l}{y=1}\\{y=\frac{1}{4}{x}^{2}-1}\end{array}\right.$可得点M(-2$\sqrt{2}$,1)、点N(2$\sqrt{2}$,1),
①当-2≤x≤2时,设点P坐标为(a,-$\frac{1}{4}$a2+1),
则PO-PD=$\sqrt{{a}^{2}+(-\frac{1}{4}{a}^{2}+1)^{2}}$-[1-(-$\frac{1}{4}$a2+1)]
=$\frac{1}{4}$a2+1-$\frac{1}{4}$a2
=1;
②当-2$\sqrt{2}$≤x<-2或2$<x≤2\sqrt{2}$时,设点P的坐标为(a,$\frac{1}{4}$a2-1),
则PO-PD=$\sqrt{{a}^{2}+(\frac{1}{4}{a}^{2}-1)^{2}}$-[1-($\frac{1}{4}$a2-1)]
=$\frac{1}{4}$a2+1-2+$\frac{1}{4}$a2
=$\frac{1}{2}$a2-1;
③当x<-2$\sqrt{2}$或x>2$\sqrt{2}$时,设点P的坐标为(a,$\frac{1}{4}$a2-1),
则PO-PD=$\sqrt{{a}^{2}+(\frac{1}{4}{a}^{2}-1)^{2}}$-[($\frac{1}{4}$a2-1)-1]
=$\frac{1}{4}$a2+1-$\frac{1}{4}$a2+2
=3;
综上,当x<-2$\sqrt{2}$、-2≤x≤2或x>2$\sqrt{2}$时,PO与PD的差为定值.
点评 本题主要考查待定系数法求二次函数的解析式、坐标与图形的变化及两点间距离公式,分类讨论思想的运用是解题的关键.


科目:初中数学 来源: 题型:填空题
 如图,矩形纸片ABCD的边AB=3,BC=4,点P是BC边上一动点(不与B、C重合),现将△ABP沿AP翻折,得到△AFP,再在CD边上选择适当的点E,将△PCE沿PE翻折,得到△PME,且直线PF、PM重合,若点F落在矩形纸片的内部,则CE的最大值是$\frac{4}{3}$.
如图,矩形纸片ABCD的边AB=3,BC=4,点P是BC边上一动点(不与B、C重合),现将△ABP沿AP翻折,得到△AFP,再在CD边上选择适当的点E,将△PCE沿PE翻折,得到△PME,且直线PF、PM重合,若点F落在矩形纸片的内部,则CE的最大值是$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 33 | B. | 32 | C. | 31 | D. | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在靠墙(墙长为18m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为36m,机场平行于墙的一边长y(m)与垂直于墙的一边a(m)的函数关系式是y=-2a+36;自变量a的取值范围是9≤a≤18.
如图,在靠墙(墙长为18m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为36m,机场平行于墙的一边长y(m)与垂直于墙的一边a(m)的函数关系式是y=-2a+36;自变量a的取值范围是9≤a≤18.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com