
【题目】在矩形![]() 中,
中,![]() 为
为![]() 的中点,一块足够大的三角板的直角顶点与点
的中点,一块足够大的三角板的直角顶点与点![]() 重合,将三角板绕点
重合,将三角板绕点![]() 旋转,三角板的两直角边分别交
旋转,三角板的两直角边分别交![]() 或它们的延长线)于点
或它们的延长线)于点![]() ,设
,设![]() ,下列四个结论:①
,下列四个结论:①![]() ;②
;②![]() ; ③
; ③![]() ;④
;④![]() ,正确的个数是( )
,正确的个数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
过点G作GH⊥BC于H,可证四边形ABHG是矩形,可得AB=GH=1,AG=BH=1,∠AGH=90°=∠EGF,由“ASA”可证△AEG≌△HFG,可得AE=HF,GE=GF,∠AEG=∠BFG,即可判断②;由旋转的性质可得点F的位置不确定,可判断①③;由锐角三角函数可得GE=![]() =
=![]() ,可求出△GEF的面积,可判断④,即可求解.
,可求出△GEF的面积,可判断④,即可求解.
解:如图,过点G作GH⊥BC于H,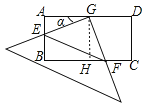
∵在矩形ABCD中,AD=2,AB=1,G为AD的中点,
∴∠A=∠B=90°,AG=DG=1=AB,
又∵GH⊥BC,
∴四边形ABHG是矩形,
∴AB=GH=1,AG=BH=1,∠AGH=90°=∠EGF,
∴∠AGE=∠FGH,
又∵∠A=∠GHF=90°,AG=GH=1,
∴△AEG≌△HFG(ASA)
∴AE=HF,GE=GF,∠AEG=∠BFG,故②正确,
∵将三角板绕点G旋转,三角板的两直角边分别交AB、BC(或它们的延长线)于点E、F,
∴点F的位置不确定,
∴HF不一定等于CF,
∴AE不一定等于CF,故①不正确,
若点F在线段CH上时,CH=HF+CF=AE+CF=1,
若点F在HC的延长线上时,CH=HF-CF=AE-CF=1,
故③不正确,
在Rt△AEG中,GE=![]() =
=![]() ,
,
∵GE=GF,∠EGF=90°,
∴S△EFG=![]() EG2=
EG2=![]() ×
×![]() .
.
故④不正确,
故选:A.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源: 题型:
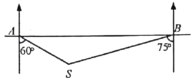
【题目】一艘轮船在![]() 处测得灯塔
处测得灯塔![]() 在船的南偏东60°方向,轮船继续向正东航行30海里后到达
在船的南偏东60°方向,轮船继续向正东航行30海里后到达![]() 处,这时测得灯塔
处,这时测得灯塔![]() 在船的南偏西75°方向,则灯塔
在船的南偏西75°方向,则灯塔![]() 离观测点
离观测点![]() 、
、![]() 的距离分别是( )
的距离分别是( )
A.![]() 海里、15海里B.
海里、15海里B.![]() 海里、15海里
海里、15海里
C.![]() 海里、
海里、![]() 海里D.
海里D.![]() 海里、
海里、![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对学生的成长有着深远的影响.某中学为了解学生每周课余阅读的时间,在本校随机抽取若干名学生进行调查,并依据调查结果经制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A |
| 6 |
|
B |
|
|
|
C |
| 10 |
|
D |
| 8 |
|
E |
| 4 |
|
合计 | 1 |
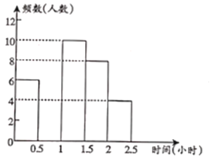
请根据图表中的信息,解答下列问题:
(1)表中的![]() ,
,![]() ,将频数分布直方图补全;
,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足1小时的学生大约有多少名?
(3)![]() 组的4人中,有1名男生和3名女生,该校计划在
组的4人中,有1名男生和3名女生,该校计划在![]() 组学生中随机选出两人向全校同学作读书心得报告,求抽取的两名学生刚好是1名男生和1名女生的概率.
组学生中随机选出两人向全校同学作读书心得报告,求抽取的两名学生刚好是1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,![]() ,
,![]() ,
,![]() 为格点,
为格点,![]() 为小正方形边的中点.
为小正方形边的中点.
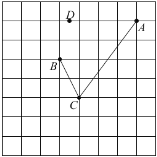
(1)![]() 的长等于_________;
的长等于_________;
(2)点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点,当
上的动点,当![]() 取得最小值时,请在如图所示的网格中,用无刻度的直尺,画出线段
取得最小值时,请在如图所示的网格中,用无刻度的直尺,画出线段![]() ,
,![]() ,并简要说明点
,并简要说明点![]() 和点
和点![]() 的位置是如何找到的(不要求证明).
的位置是如何找到的(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线G:y1=a(x+1)2+2与H:y2=﹣(x﹣2)2﹣1交于点B(1,﹣2),且分别与y轴交于点D、E.过点B作x轴的平行线,交抛物线于点A、C,则以下结论:①无论x取何值,y2总是负数;②抛物线H可由抛物线G向右平移3个单位,再向下平移3个单位得到;③当﹣3<x<1时,随着x的增大,y1﹣y2的值先增大后减小;④四边形AECD为正方形.其中正确的是( )

A.①③④B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
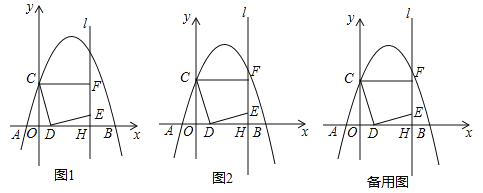
(1)求抛物线解析式;
(2)如图2,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:
①连接DF,求tan∠FDE的值;
②试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
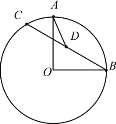
【题目】如图,已知⊙O的半径是2,点A,B在⊙O上,且∠AOB=90°,动点C在⊙O上运动(不与A,B重合),点D为线段BC的中点,连接AD,则线段AD的长度最大值是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
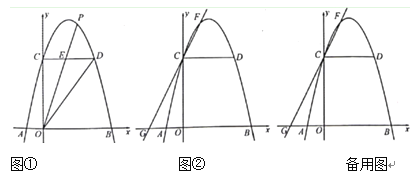
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,
,![]() (
(![]() 在
在![]() 左侧),与
左侧),与![]() 轴正半轴交于点
轴正半轴交于点![]() ,点
,点![]() 在抛物线上,
在抛物线上,![]() 轴,且
轴,且![]() .
.
(1)求点![]() ,
,![]() 的坐标及
的坐标及![]() 的值;
的值;
(2)点![]() 为
为![]() 轴右侧抛物线上一点.
轴右侧抛物线上一点.
①如图①,若![]() 平分
平分![]() ,
,![]() 交
交![]() 于点
于点![]() ,求点
,求点![]() 的坐标;
的坐标;
②如图②,抛物线上一点![]() 的横坐标为2,直线
的横坐标为2,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com