
����Ŀ��Ϊ���˽������еĿ��������������У��2017�����ۺ�ʵ���������顱С��ӻ�������������ȡ��������Ŀ���������Ϊ��������ͳ�ƣ���������ͼ��ʾ������ͳ��ͼ������ͳ��ͼ��������Ϣδ��������


��1������С�������ȡ������Ϊ_______�죬�뽫����ͳ��ͼ����������
��2��Ϊ�ҳ��Ż������Ĵ�ʩ����������������С�顱��ͬѧ������������Ϊ���ж���Ⱦ���͡��ض���Ⱦ���������������ȡ���������Ⱦԭ�������б�����״ͼ�ķ����������ȡ������ǡ�ö��ǡ��ض���Ⱦ���ĸ��ʣ�
���𰸡�(1)60��ͼ���ԣ���2��![]()
��������������(1)��������Ϊ��������������12������ռ�İٷֱ�Ϊ20%�������ȡ���������ֱ������Ⱥ�����������ɲ�ȫ����ͼ��(2)���б��������.
��⣺(1)����С�������ȡ������Ϊ12��20%��60�죬�������Ⱦ������Ϊ60��5%��3�죬����Ⱦ������Ϊ60��12��36��3��2��2��5�죬����ͼ�������£�

(2)�������⣬�б���
�ж�1 | �ж�2 | �ض�1 | �ض�2 | |
�ж�1 | �ж�1���ж�2 | �ж�1���ض�1 | �ж�1���ض�2 | |
�ж�2 | �ж�2���ж�1 | �ж�2���ض�1 | �ж�2���ض�2 | |
�ض�1 | �ض�1���ж�1 | �ض�1���ж�2 | �ض�1���ض�2 | |
�ض�2 | �ض�2���ж�1 | �ض�2���ж�2 | �ض�2���ض�1 |
�ɱ���֪������12�ֵȿ����ԣ����з�����������2����
����P(����ǡ�ö��ǡ��ض���Ⱦ��)��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽����
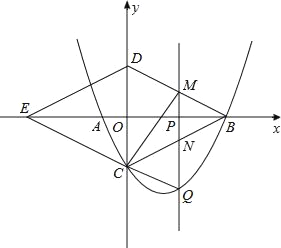
��ͼ��������y=![]() x2��
x2��![]() x��4��x�ύ��A��B���㣨��B�ڵ�A���Ҳࣩ����y�ύ�ڵ�C������BC����BCΪһ�ߣ���OΪ�Գ�����������BDEC����P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q��
x��4��x�ύ��A��B���㣨��B�ڵ�A���Ҳࣩ����y�ύ�ڵ�C������BC����BCΪһ�ߣ���OΪ�Գ�����������BDEC����P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q��
��1�����A��B��C�����꣮
��2������P���߶�OB���˶�ʱ��ֱ��l�ֱ�BD��BC�ڵ�M��N����̽��mΪ��ֵʱ���ı���CQMD��ƽ���ı��Σ���ʱ�����ж��ı���CQBM����״����˵�����ɣ�
��3������P���߶�EB���˶�ʱ���Ƿ���ڵ�Q��ʹ��BDQΪֱ�������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������̨�����н�Լ�������˷ѡ�����涨��ijƷ�Ƹߵ�������������������·ݺ�����Ϊ����������ÿƿ��![]() �����·ݽ���500Ԫ�����������ͬ�����ĸߵ���
�����·ݽ���500Ԫ�����������ͬ�����ĸߵ���![]() �����·����۶�Ϊ4.5��Ԫ�����·����۶�ֻ��3��Ԫ.
�����·����۶�Ϊ4.5��Ԫ�����·����۶�ֻ��3��Ԫ.
��1�������·�ÿƿ�ߵ���![]() �ۼ�Ϊ����Ԫ��
�ۼ�Ϊ����Ԫ��
��2��Ϊ��������þ����̼ƻ����·ݹ������ִ��ڻ����е͵���![]() ����.��֪�ߵ���
����.��֪�ߵ���![]() ÿƿ����Ϊ800Ԫ���е͵���
ÿƿ����Ϊ800Ԫ���е͵���![]() ÿƿ����Ϊ400Ԫ.���ò�����5.5��Ԫ��Ԥ���ʽ�
ÿƿ����Ϊ400Ԫ.���ò�����5.5��Ԫ��Ԥ���ʽ�![]() ��
��![]() ���־ƹ�100ƿ���Ҹߵ���
���־ƹ�100ƿ���Ҹߵ���![]() ���ٹ���35ƿ�������˵���м��ֽ���������
���ٹ���35ƿ�������˵���м��ֽ���������
��3�����̳��ƻ����¶Ըߵ���![]() ���д�����������������ۼۻ�����ÿ�۳�һƿ�ߵ���
���д�����������������ۼۻ�����ÿ�۳�һƿ�ߵ���![]() ���˿ͼ�ֵ
���˿ͼ�ֵ![]() Ԫ�Ĵ���ȯ�����е͵���
Ԫ�Ĵ���ȯ�����е͵���![]() ���ۼ�Ϊ550Ԫ/ƿ.Ҫʹ��2�������з�������ǡ����ͬ����ȷ��
���ۼ�Ϊ550Ԫ/ƿ.Ҫʹ��2�������з�������ǡ����ͬ����ȷ��![]() ��ֵ����˵����ʱ���ַ����Ծ����̸�������
��ֵ����˵����ʱ���ַ����Ծ����̸�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���糿�ܲ��������Լ��ҳ�����������2km����С��ң�����������1.5km����С��ң�Ȼ������������4.5km����ѧУ����������ܻص��Լ��ң�
��1����С����Ϊԭ�㣬����Ϊ��������1����λ���ȱ�ʾ1km����ͼ�е������ϣ��ֱ��õ�A��ʾ��С��ң��õ�B��ʾ��С��ң��õ�C��ʾ��ѧУ��λ�ã�
![]()
��2����С�����ѧУ֮��ľ��룻
��3�����С���ܲ����ٶ���250m/min����ôС���ܲ�һ�����˶ʱ�䣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Բ�İ뾶Ϊ![]() ����λ���ȣ�������ÿ������֮��ľ���Ϊ1����λ���ȣ���Բ��4�ȷֵ㴦�ֱ���ϵ�A��B��C��D������Բ���ϵĵ�A�������ϱ�ʾ-1�ĵ��غϣ�
����λ���ȣ�������ÿ������֮��ľ���Ϊ1����λ���ȣ���Բ��4�ȷֵ㴦�ֱ���ϵ�A��B��C��D������Բ���ϵĵ�A�������ϱ�ʾ-1�ĵ��غϣ�
(1)Բ���ܳ�Ϊ���٣�
(2)����Բ�����������ҹ���2�ܺ������A�غϵĵ��ʾ����Ϊ���٣�
(3)�������ᰴ��˳ʱ�뷽�����ڸ�Բ�ϣ����������ϱ�ʾ-2�ĵ����B�غϣ������ϱ�ʾ-3�ĵ����C�غϡ�������ô�����ϱ�ʾ-2018�ĵ���Բ�����ĸ����غϣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=3��AC=4��BC=5��PΪ��BC��һ���㣬PE��AB��E��PF��AC��F��MΪEF�е㣬��AM����СֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���O�DZ�AC��һ�����㣬��O��ֱ��MN��BC����MN����ACB��ƽ�����ڵ�E������ACB�����ƽ�����ڵ�F��
��1����֤��OE��OF��
��2������O�ڱ�AC���˶���ʲôλ��ʱ���ı���AECF�Ǿ��Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ɶ������Ǽ���ѧ��һ�Ź�ʶ�Ŀ�����飬����Ϊ������ѧ�Ļ�ʯ�����й��Ƿ��ֺ��о����ɶ�������ϵĹ���֮һ���й��Ŵ���ѧ�ҳ�ֱ��������Ϊ�����Σ��϶̵�ֱ�DZ߳�Ϊ������һֱ�DZ߳�Ϊ�ɣ�б�߳�Ϊ�ң����Թ��ɶ���Ҳ��Ϊ�����Ҷ���������ʱ�������ˬ������������Բ��ͼ������ͼ��֤���˹��ɶ����������������Բ��ͼ���У���������ABCD����4��ȫ�ȵ�ֱ���������ټ����м���Ǹ�С������EFGH��ɵģ���С�����εı߳���1��ÿ��ֱ�������εĶ̵�ֱ�DZ߳���3�����������ABCD�������_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�濿ǽ�Ŀյ��ϣ��ó�Ϊ24�����Χ���м���ж�����ʵij����λ��ԣ�����Ƶ����۽Ƕȳ�����ǽ����С���ó���Ϊ4�ף�ǽ�������ó���Ϊ14�ף�
��1������Χ�ɵĻ��Ե����Ϊ32ƽ���ף����ԵĿ�AB�ij��ȣ�
��2����AB�ij�Ϊ�� ��ʱ����Χ�ɵĻ������������ֵΪ�� ����2����AB�ij�Ϊ�� ��ʱ����Χ�ɵĻ��������С����СֵΪ�� ����2��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com