
阅读理解填空:
(1)如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.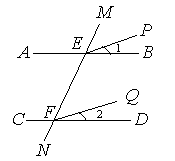
证明:∵AB∥CD,
∴∠MEB=∠MFD( )
又∵∠1=∠2,
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠______
∴EP∥_____.( )
(2)如图,EF∥AD,∠1=∠2,∠BAC=70 o,求∠AGD.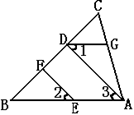
解:∵EF∥AD,
∴∠2= ( )
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥ ( )
∴∠BAC+ =180 o( )
∵∠BAC=70 o,
∴∠AGD= 。
(1)两直线平行,同位角相等;MFQ;FQ;同位角相等,两直线平行
(2)∠3;两直线平行,同位角相等;DG;内错角相等,两直线平行;∠AGD;两直线平行,同旁内角互补;110°
解析试题分析:根据平行线的判定和性质依次分析即可.
(1)∵AB∥CD,
∴∠MEB=∠MFD(两直线平行,同位角相等)
又∵∠1=∠2,
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠MFQ
∴EP∥FQ(同位角相等,两直线平行);
(2)∵EF∥AD,
∴∠2=∠3(两直线平行,同位角相等)
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥DG(内错角相等,两直线平行)
∴∠BAC+∠AGD =180 o(两直线平行,同旁内角互补)
∵∠BAC=70 o,
∴∠AGD=110°.
考点:本题考查的是平行线的判定和性质
点评:解答本题的关键是熟练掌握两直线平行,同位角相等,两直线平行,同旁内角互补;同位角相等,两直线平行.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:阅读理解
| (2x-y)2 |
| 3 | (x-2y)3 |
| 3x+y |
| x-y |
| (2x-y)2 |
| 3 | (x-2y)3 |
|
|
| 3x+y |
| x-y |
| 3x+y |
| x-y |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| -1+2+3 |
| 3 |
| 4 |
| 3 |
|

| 26 |
| 1 |
| 2 |
| 26 |
| 26 |
| 8 |
| 3 |
| 8 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:2012-2013年海南洋浦中学七年级上期末考试数学试卷(解析版) 题型:解答题
阅读理解填空:
(1)如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.
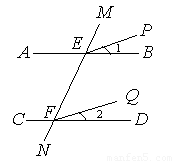
证明:∵AB∥CD,
∴∠MEB=∠MFD( )
又∵∠1=∠2,
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠______
∴EP∥_____.( )
(2)如图,EF∥AD,∠1=∠2,∠BAC=70 o,求∠AGD.

解:∵EF∥AD,
∴∠2= ( )
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥ ( )
∴∠BAC+ =180 o( )
∵∠BAC=70 o,
∴∠AGD= 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com