Question

16．定义：有一组对角互补的四边形叫做互补四边形
（1）互补四边形ABCD中，若∠B：∠C：∠D=2：3：4，则∠A=90°；
（2）已知：如图1，在四边形ABCD中，BD平分∠ABC，AD=CD，BC＞BA．求证：四边形ABCD是互补四边形；
（3）如图2，互补四边形ABCD中，∠B=∠D=90°，AB=AD=2$\sqrt{3}$，点E，F分别是边BC，CD的动点，且∠EAF=$\frac{1}{2}$∠BAD=60°，△CEF周长是否变化？若不变，请求出不变的值；若有变化，说明理由；
（4）如图3，互补四边形ABCD中，∠A=∠C=90°，AB=BC，∠B=150°，将纸片先沿直线BD对折，再将对折后的图形沿从一个顶点出发的直线裁剪，剪开后的图形打开铺平，若铺平后的图形中有一个是面积为2的平行四边形，求CD的长；

Answer 1

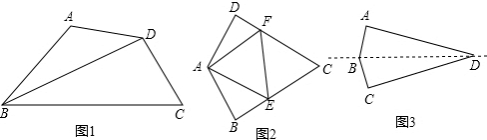
分析 （1）由互补四边形和四边形内角和定理即可求出∠A的度数；
（2）在BC上截取BE=BA，连接DE，证明△BAD≌△BED．得出∠A=∠DEB，AD=DE．证出DE=DC．由等腰三角形的性质得出∠C=∠DEC，即可得出结论；
（3）延长CB到G，使BG=DF，连接AG，由互补四边形的定义得出∠ADC=180°-∠ABC=30°，由SAS证明△ABG≌△ADF，得出∠BAG=∠DAF，AG=AF，再由已知得出∠EAF=∠EAG，由SAS证明△AEF≌△AEG，得出EF=EG=EB+BG=EB+DF．CE+CE+CF=BC+CD，连接AC，由三角形全等得出BC=CD=6，即可得出结果；
（4）分两种情况：①证明四边形BMDN是菱形，得出BN=BM=DM，∠MBN=∠ADC=30°，设BM=BN=DM=2x，作NH⊥BM于H，则NH=$\frac{1}{2}$BN=x，由菱形的面积得出x=$\sqrt{1}$=1，求出BM=DM=2，BC=$\frac{1}{2}$BM=1，CM=$\sqrt{3}$BC=$\sqrt{3}$，即可得出CD的长；
②同①得：△BAD≌△BCD，四边形ABCE是菱形，AB=AE=2，∴AD=CD，∠ABD=∠AEB=75°，由三角形内角和求出∠BAE=30°，作EF⊥AE交AD于F，则∠AFE=30°，由含30°角的直角三角形的性质得出AF=2AE=4，EF=$\sqrt{3}$AE=2$\sqrt{3}$，由三角形的外角性质和等腰三角形的判定得出DF=EF=2$\sqrt{3}$，即可求出CD的长．

解答 （1）解：∵四边形ABCD是互补四边形，
∴∠B+∠D=180°，
∵∠B：∠C：∠D=2：3：4，
∴∠B=60°，∠C=90°，
又∵∠A+∠B+∠C+∠D=360°，
∴∠A=180°-∠C=90°；
故答案为：90；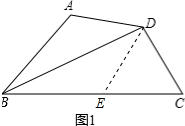
（2）证明：在BC上截取BE=BA，连接DE，如图1所示：
在△BAD和△BED中，$\left\{\begin{array}{l}{BA=BE}&{\;}\\{∠ABD=∠CBD}&{\;}\\{BD=BD}&{\;}\end{array}\right.$，
∴△BAD≌△BED（SAS），
∴∠A=∠DEB，AD=DE．
∵AD=CD，
∴DE=DC．∴∠C=∠DEC．
∵∠BED+∠DEC=180°，
∴∠A+∠C=180°，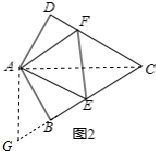
∴四边形ABCD是互补四边形；
（3）解：不变．理由如下：
延长CB到G，使BG=DF，连接AG，
∵四边形ABCD是互补四边形，
∴∠ADC=180°-∠ABC=30°，
∵∠ABE=∠D=90°，
∴∠ABG=∠D=90°，
在△ABG和△ADF中，$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠ABG=∠D}&{\;}\\{BG=DF}&{\;}\end{array}\right.$
∴△ABG≌△ADF（SAS），
∴∠BAG=∠DAF，AG=AF，
∵∠EAF=$\frac{1}{2}$∠BAD，
∴∠DAF+∠BAE=∠EAF，
∴∠EAF=∠EAG，
在△AEF和△AEG中，$\left\{\begin{array}{l}{AF=AG}&{\;}\\{∠EAF=∠EAG}&{\;}\\{AE=AE}&{\;}\end{array}\right.$，
∴△AEF≌△AEG（SAS），
∴EF=EG=EB+BG=EB+DF．
∴CE+CE+CF=BC+CD，
连接AC，在Rt△ABC和Rt△ADC中，$\left\{\begin{array}{l}{AC=AC}\\{AB=AD}\end{array}\right.$，
∴Rt△ABC≌Rt△ADC（HL），
∴BC=CD=6，
∴△CEF的周长=EF+CE+CF=BC+CD=12；
（4）解：分两种情况：
①如图3所示：四边形BMDN是平行四边形，
∴BM∥AD，
∴∠MBD=∠NDB，同（3）得：Rt△BCD≌Rt△BAD（HL），
∴∠MDB=∠NDB，
∴∠MBD=∠MDB，
∴BM=DM，
∴四边形BMDN是菱形，
∴BN=BM=DM，∠MBN=∠ADC=30°，
设BM=BN=DM=2x，
作NH⊥BM于H，则NH=$\frac{1}{2}$BN=x，
∵菱形BMDN的面积=BM•NH=2x•x=2，
解得：x=$\sqrt{1}$=1，
∴BM=DM=2，
∵∠BMC=∠ADC=30°，∠BCD=90°，
∴BC=$\frac{1}{2}$BM=1，CM=$\sqrt{3}$BC=$\sqrt{3}$，
∴CD=DM+CM=2+$\sqrt{3}$；
②如图4所示：同①得：△BAD≌△BCD，四边形ABCE是菱形，AB=AE=2，
∴AD=CD，∠ABD=∠AEB=75°，
∴∠BAE=30°，
∵∠BAD=90°，
∴∠DAE=60°，
作EF⊥AE交AD于F，则∠AFE=30°，
∴AF=2AE=4，
∴EF=$\sqrt{3}$AE=2$\sqrt{3}$，
由三角形的外角性质得：∠FED=∠FDE=15°，
∴DF=EF=2$\sqrt{3}$，
∴CD=AD=AF+DF=4+2$\sqrt{3}$；
综上所述：CD的长为$2+\sqrt{3}$或$4+2\sqrt{3}$．

点评 本题是四边形综合题目，考查了互补四边形的判定与性质、全等三角形的判定与性质、含30°角的直角三角形的性质、勾股定理、等腰三角形的判定的判定与性质等知识；本题综合性强，有一定难度，证明三角形全等是解决问题的关键．