
【题目】如图,点![]() 是
是![]() 的外角平分线上一点,且满足
的外角平分线上一点,且满足![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中正确的结论有( )
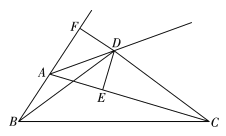
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
根据角平分线上的点到角的两边距离相等可得DE=DF,再利用“HL”证明Rt△CDE和Rt△BDF全等;根据全等三角形对应边相等可得CE=AF,利用“HL”证明Rt△ADE和Rt△ADF全等,根据全等三角形对应边相等可得AE=AF,然后求出CE=AB+AE;根据全等三角形对应角相等可得∠DBF=∠DCE,然后求出A、B、C、D四点共圆,根据同弧所对的圆周角相等可得∠BDC=∠BAC;∠DAE=∠CBD,再根据全等三角形对应角相等可得∠DAE=∠DAF,然后求出∠DAF=∠CBD,进而得出∠ADF=∠CDB,不能得出∠ADF=∠CDE.
解:∵AD平分∠CAF,DE⊥AC,DF⊥AB,
∴DE=DF,
在Rt△CDE和Rt△BDF中,
![]()
∴Rt△CDE≌Rt△BDF(HL),故①正确;
∴CE=AF,
在Rt△ADE和Rt△ADF中,
![]()
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,
∴CE=AB+AF=AB+AE,故②正确;
∵Rt△CDE≌Rt△BDF,
∴∠DBF=∠DCE,
∴A、B、C、D四点共圆,
∴∠BDC=∠BAC,故④正确;
∠DAE=∠CBD,
∵Rt△ADE≌Rt△ADF,
∴∠DAE=∠DAF,
∴∠DAF=∠CBD,
∵BD=CD,
∴∠DBC=∠DCB,
∴∠ADF=∠CAD,
∴∠ADF≠∠CDE,故③错误;
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣ ![]() x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0).
x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0).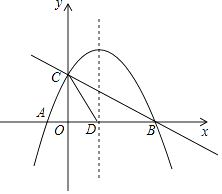
(1)求抛物线的解析式;
(2)抛物线的对称轴与x轴交于点D,连接CD,点P是直线BC上方抛物线上的一动点(不与B,C重合),当点P运动到何处时,四边形PCDB的面积最大?求出此时四边形PCDB面积的最大值和点P坐标;
(3)在抛物线上的对称轴上:是否存在一点M,使|MA﹣MC|的值最大;是否存在一点N,使△NCD是以CD为腰的等腰三角形?若存在,直接写出点M,点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清晨,张强从家跑步去迎泽公园,在公园锻炼了一段时间后,又去附近早餐店吃早餐,然后散步走回家.下图反映了这段时间内,张强离家的距离随离家时间的变化而变化的情况,其中![]() (分)表示张强离家时间,
(分)表示张强离家时间,![]() (千米)表示他离家的距离.根据图象所反映的信息,以下四个说法正确的是( )
(千米)表示他离家的距离.根据图象所反映的信息,以下四个说法正确的是( )
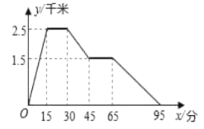
①迎泽公园离张强家2.5千米.
②张强在迎泽公园锻炼了15分钟.
③迎泽公园离早餐店4千米.
④张强从早餐店回家的平均速度是3千米/小时.
A.①②B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2a ,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按如图2的形状拼成一个正方形.
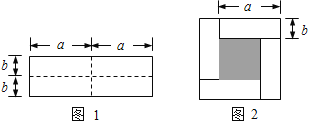
(1)图2的阴影部分的正方形的边长是 ______.
(2)用两种不同的方法求图中阴影部分的面积.
(方法1)![]() = _____________;
= _____________;
(方法2)![]() =______________;
=______________;
(3)观察如图2,写出(a+b)2,(a-b)2,ab这三个代数式之间的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.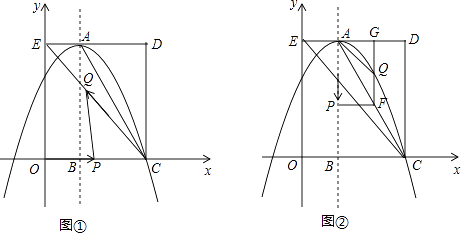
(1)填空:点A坐标为;抛物线的解析式为 .
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若﹣ ![]() a≥b,则a≤﹣2b,其根据是( )
a≥b,则a≤﹣2b,其根据是( )
A.不等式的两边都加上(或减去)同一个整式,不等号的方向不变
B.不等式的两边都乘(或除以)同一个正数,不等号的方向不变
C.不等式的两边都乘(或除以)同一个负数,不等号的方向改变
D.以上答案均不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校利用暑假进行田径场的改造维修,项目承包单位派遣甲施工队进场施工,计划用40天时间完成整个工程.当甲施工队工作5天后,承包单位接到通知,有一大型活动要在该田径场举行,要求比原计划提前14天完成整个工程,于是承包单位派遣乙施工队与甲施工队共同完成剩余工程,结果按通知要求如期完成了整个工程.
(1)若乙施工队单独施工,完成整个工程需要多少天?
(2)若此项工程甲、乙施工队同时进场施工,完成整个工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K-∠H=33°,则∠K=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲同学手中藏有三张分别标有数字 ![]() 、
、 ![]() 、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
(1)请你用树形图或列表法列出所有可能的结果;
(2)现制定一个游戏规则:若所选出的a,b能使得ax2+bx+1=0有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请用概率知识解释.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com