
分析 首先根据题意,要使分式$\frac{x-1}{2-3x}$的值为正数,判断出两种情况:①分式的分母、分子同时为正;②分式的分母、分子同时为负;然后根据一元一次不等式的解法,求出x的取值范围即可.
解答 解:∵分式$\frac{x-1}{2-3x}$的值为正数,
∴$\left\{\begin{array}{l}{x-1>0}\\{2-3x>0}\end{array}\right.$或$\left\{\begin{array}{l}{x-1<0}\\{2-3x<0}\end{array}\right.$,
(1)当$\left\{\begin{array}{l}{x-1>0}\\{2-3x>0}\end{array}\right.$时,不等式组无解;
(2)当$\left\{\begin{array}{l}{x-1<0}\\{2-3x<0}\end{array}\right.$时,
解得$\frac{2}{3}<x<1$,
综上,可得x的取值范围是:$\frac{2}{3}<x<1$.
故答案为:$\frac{2}{3}<x<1$.
点评 (1)此题主要考查了分式的值的正负性的判断,考查了分类讨论思想的应用,解答此题的关键是要明确分式$\frac{x-1}{2-3x}$的值为正数的两种情况:①分式的分母、分子同时为正;②分式的分母、分子同时为负.
(2)此题还考查了一元一次不等式的求解问题,要熟练掌握求解的方法.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2y2+y-1=0 | B. | $\frac{1}{{x}^{2}}$-2x=1 | C. | ax2+bx+c=0 | D. | $\frac{1}{2}$x2=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<11 | B. | m>11 | C. | m≤11 | D. | m≥11 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
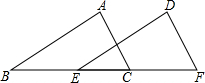 如图,在△ABC和△DEF中,已知AC=DF,∠A=∠D,要使△ABC≌△DEF,下列条件不行的( )
如图,在△ABC和△DEF中,已知AC=DF,∠A=∠D,要使△ABC≌△DEF,下列条件不行的( )| A. | BC=EF | B. | ∠ACB=∠F | C. | ∠B=∠DEF | D. | AB=DE |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
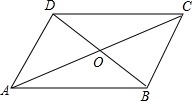 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )| A. | AB∥CD,AD∥BC | B. | AB∥CD,AD=BC | C. | AO=CO,BO=DO | D. | AB=CD,AD=BC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com