
 如图,在△ABC中,∠ACB=90°,BC=nAC,CD⊥AB于D,点P为AB边上一动点,PE⊥AC,PF⊥BC,垂足分别为E、F.
如图,在△ABC中,∠ACB=90°,BC=nAC,CD⊥AB于D,点P为AB边上一动点,PE⊥AC,PF⊥BC,垂足分别为E、F.分析 (1)根据∠ACB=90°,PE⊥AC,PF⊥BC,那么CEPF就是个矩形.得到CE=PF从而不难求得CE:BF的值;
(2)可通过构建相似三角形来求解;
(3)可根据(2)的思路进行反向求解,即先通过EF,DF的比例关系,求出DE:DF的值.也就求出了CE:BF的值即tanB=AC:BC的值.
解答 解:(1)∵∠ACB=90?,PE⊥AC,PF⊥BC,
∴四边形CEPF是矩形.
∴CE=PF.
∴CE:BF=PF:BF=tanB=AC:BC=$\frac{1}{2}$.
故答案是:$\frac{1}{2}$.
(2)连DE,∵∠ACB=90°,PE⊥CA,PF⊥BC,
∴四边形CEPF是矩形.
∴CE=PF.
∴CE:BF=CD:BD=PF:BF=tanB.
∵∠ACB=90?,CD⊥AB,
∴∠B+∠A=90°,∠ECD+∠A=90°,
∴∠ECD=∠B,
∴△CED∽△BFD.
∴∠EDC=∠FDB.
∵∠FDB+∠CDF=90°,
∴∠CDE+∠CDF=90°.
∴∠EDF=90°.
∵$\frac{DE}{DF}$=tanB=$\frac{1}{3}$,设DE=a,DF=3a,
在直角三角形EDF中,根据勾股定理可得:EF=$\sqrt{10}$a.
∴$\frac{EF}{DF}$=$\frac{\sqrt{10}a}{3a}$=$\frac{{\sqrt{10}}}{3}$.
(3)可根据(2)的思路进行反向求解,即先通过EF,DF的比例关系,求出DE:DF的值.也就求出了CE:BF的值,即tanB=$\frac{AC}{BC}$=$\sqrt{3}$.
点评 本题主要考查了相似综合题,通过相似三角形将所求线段之间的比例关系同已知的线段间的比例关系联系在一起是解题的关键.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:解答题
 如图所示,已知△ABC,D在BC的延长线上,E在CA的延长线上,F在AB上,∠ACD=130°,∠AFE=60°,∠B=∠E,求∠B的度数.
如图所示,已知△ABC,D在BC的延长线上,E在CA的延长线上,F在AB上,∠ACD=130°,∠AFE=60°,∠B=∠E,求∠B的度数.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知:如图,矩形ABCD的边AB=3,AD=4,若以点A为圆心画⊙A.
已知:如图,矩形ABCD的边AB=3,AD=4,若以点A为圆心画⊙A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 跳绳时绳甩到最高处时的形状是抛物线,如图,正在甩绳的甲、乙两同学拿绳的手到地面的距离均为0.9米,小丽站在距离点O的水平距离为1米的F处,绳子甩到最高处时刚好通过她的头顶E,以O为原点建立如图所示的平面直角坐标系,已知抛物线的解析式为y=-0.1x2+0.6x+0.9.
跳绳时绳甩到最高处时的形状是抛物线,如图,正在甩绳的甲、乙两同学拿绳的手到地面的距离均为0.9米,小丽站在距离点O的水平距离为1米的F处,绳子甩到最高处时刚好通过她的头顶E,以O为原点建立如图所示的平面直角坐标系,已知抛物线的解析式为y=-0.1x2+0.6x+0.9.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
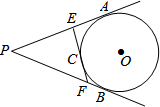 如图,PA、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点为C,若PA=5cm,则△PEF的周长为10cm.
如图,PA、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点为C,若PA=5cm,则△PEF的周长为10cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com