
【题目】如图,AB为⊙O的直径,C,E为⊙O上的两点,AC平分∠EAB,CD⊥AE于D.
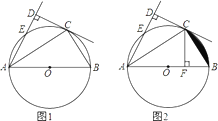
(1)求证:CD为⊙O的切线;
(2)过点C作CF⊥AB于F,如图2,判断CF和AF,DE之间的数量关系,并证明之;
(3)若AD-OA=1.5,AC=3![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)证明见解析;(2)CF2=AFDE;(3)![]() .
.
【解析】
(1)连接OC,如图1,由AC平分∠EAB得到∠1=∠2,加上∠2=∠3,则∠1=∠3,于是可判断OC∥AD,则有AD⊥CD可判断OC⊥CD,然后根据切线的判定定理得到CD为⊙O的切线;
(2)连结CE,如图2,根据角平分线的性质得CD=CF,再证明Rt△ACD≌△ACF得到AD=AF,接着证明Rt△DEC∽Rt△DCA,理由相似得性质得DE:DC=DC:DA,然后利用等线段代换即可得到CF2=DEAF;
(3)设⊙O的半径为r,由AD=AF,AD-OA=1.5可得到OF=1.5,再证明Rt△ACF∽Rt△ABC,利用相似比可计算出r=3,接着在Rt△FCO中,利用余弦的定义可求出∠COB=60°,然后根据扇形的面积公式和等边三角形面积公式和S阴影部分=S扇形BOC-S△BOC进行计算即可.
(1)解:连接OC,如图1.
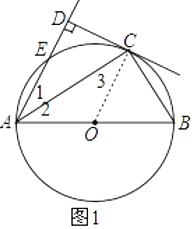
∵AC平分∠EAB,
∴∠1=∠2.
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
∴OC∥AD.
∵AD⊥CD,
∴OC⊥CD,
∴CD为⊙O的切线;
(2)解:CF2=AFDE.理由如下:
连结CE,如图2.
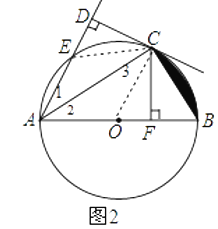
∵AC平分∠EAB,CD⊥AE,CF⊥AB,
∴CD=CF.
在Rt△ACD和△ACF中,![]() ,
,
∴Rt△ACD≌△ACF,
∴AD=AF.
∵四边形CEAB内接于⊙O,
∴∠DEC=∠B.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ABC+∠2=90°,∠1+∠ACD=90°,∠1=∠2,
∴∠DEC=∠ACD,
∴Rt△DEC∽Rt△DCA,
∴DE:DC=DC:DA,
∴DC2=DEDA,
∴CF2=DEAF;
(3)解:设⊙O的半径为r.
∵AD=AF,而AD﹣OA=1.5,
∴AF=AD=OA+OF=r+1.5,∴OF=1.5.
∵∠CAB=∠FAC,
∴Rt△ACF∽Rt△ABC,
∴ ![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:r=3或r=-![]() (舍去).
(舍去).
在Rt△FCO中,∵cos∠COF=![]() =
=![]() =
=![]() ,
,
∴∠COB=60°,
∴S阴影部分=S扇形BOC﹣S△BOC
=![]() -
-![]() ×32=
×32=![]() π-
π-![]() .
.
故答案为:(1)证明见解析;(2)CF2=AFDE;(3)![]() .
.


科目:初中数学 来源: 题型:
【题目】天山旅行社为吸引游客组团去具有喀斯特地貌特征的黄果树风景区旅游,推出了如下收费标准(如图所示):

某单位组织员工去具有喀斯特地貌特征的黄果树风景区旅游,共支付给旅行社旅游费用27000元,请问该单位这次共有多少名员工去具有喀斯特地貌特征的黄果树风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击教练为了了解队员训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射靶5次,成绩统计如下:
命中环数 | 6 | 7 | 8 | 9 | 10 |
甲命中相应环数的次数 | 0 | 1 | 3 | 1 | 0 |
乙命中相应环数的次数 | 2 | 0 | 0 | 2 | 1 |
(1)试通过计算说明甲、乙两人的成绩谁比较稳定?
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会 .(填“变大”、“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
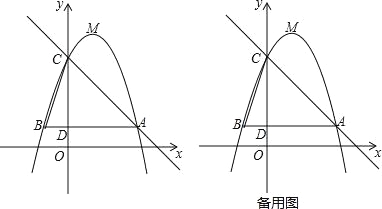
(1)求该二次函数的解析式及点M的坐标;
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;
(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x-m)2-2a(x-m)(a,m为常数,且a≠0).
(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;
(2)设该函数的图象的顶点为C,与x轴交于A,B两点,当△ABC是等腰直角三角形时,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为直角边在AD右侧作等腰直角三角形ADE,且∠DAE=90°,连接CE.

(1)如图①,当点D在线段BC上时:
①BC与CE的位置关系为 ;
②BC、CD、CE之间的数量关系为 .
(2)如图②,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若不成立,请你写出正确结论,并给予证明.
(3)如图③,当点D在线段BC的延长线上时,BC、CD、CE之间的数量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
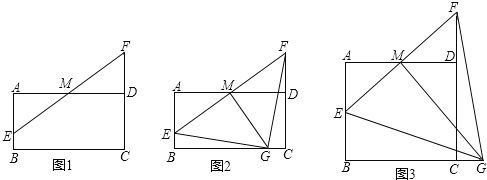
【题目】如图,在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连结EM并延长交线段CD的延长线于点F.
(1)如图1,求证:AE=DF;
(2)如图2,过点M作MG⊥EF交线段BC于点G,若ME=MG,求证:BE=CG;
(3)如图3,若AB=2![]() ,过点M作MG⊥EF交线段BC的延长线于点G.求线段AE长度的取值范围.
,过点M作MG⊥EF交线段BC的延长线于点G.求线段AE长度的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com