练习册

  • 练习册
  • 试题
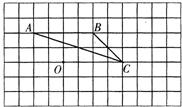
    精英家教网 > 初中数学 > 题目详情

    图中图(1)是一个10×10格点正方形组成的网格．△ABC是格点三角形(顶点在网格交点处)，请你完成下面的两个问题：

    (1)在图(1)中画出与△ABC相似的格点△A1B1C1和△A2B2C2，且△A1B1C1与△ABC的相似比是2，△A2B2C2与△ABC的相似比是；

    (2)在图(2)中用与△ABC、△A1B1C1、△A2B2C2全等的格点三角形(每个三角形至少使用一次)，拼出一个你熟悉的图案，并为你设计的图案配一句贴切的解说词．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    请阅读下列材料：
    问题：现有5个边长为1的正方形，排列形式如图①，请把它们分割后拼接成一个新的正方形，要求：画出分割线并在正方形网格图（图中每个小正方形的边长均为1）中用实线画出拼接成的新正方形．
    小东同学的做法是：设新正方形的边长为x（x＞0），依题意，割补前后图形的面积相等，有x2=5，解得x=
    		5
    ，由此可知新正方形得边长等于两个小正方形组成得矩形对角线得长，于是，画出如图②所示的分割线，拼出如图③所示的新正方形．精英家教网
    请你参考小东同学的做法，解决如下问题：
    现有10个边长为1的正方形，排列形式如图④，请把它们分割后拼接成一个新的正方形，要求：在图④中画出分割线，并在图⑤的正方形网格图（图中每个小正方形的边长均为1）中用实线画出拼接成的新正方形．（说明：直接画出图形，不要求写分析过程．）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）在2004年6月的日历中（见图），任意圈出一竖列上相邻的三个数，设中间的一个为a，则用含a的代数式表示这三个数（从小到大排列）分别是
     
    ；
    （2）连续的自然数1至2004按图中的方式派成一个长方形阵列，用一个正方形框出16个数（如图）
    ①图中框出的这16个数之和是
     
    ；
    ②在上图中，要使一个正方形框出的16个数之和分别等于2000、2004，是否可能？若不可能，试说明理由．若有可能，请求出该正方形框出的16个数中的最小数与最大数．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    27、我们约定，若一个三角形（记为△A1）是由另一个三角形（记为△A）通过一次平移，或绕其任一边的中点旋转180°得到的，则称△A1是由△A复制的．以下的操作中每一个三角形只可以复制一次，复制过程可以一直进行下去．如图1是由△A复制出△A1，又由△A1复制出△A2，再由△A2复制出△A3，形成了一个大三角形，记作△B．以下各题中的复制均是由△A开始的，由复制形成的多边形中的任意两个小三角形（指与△A全等的三角形）之间既无缝隙也无重叠．
    （1）图1中标出的是一种可能的复制结果，它用到
    1
    次平移，
    2
    次旋转．小明发现△B∽△A，其相似比为
    2：1
    ．若由复制形成的△C的一条边上有11个小三角形（指有一条边在该边上的小三角形），则△C中含有
    121
    个小三角形；
    （2）若△A是正三角形，你认为通过复制能形成的正多边形是
    正三边形、正六边形
    ；
    （3）在复制形成四边形的过程中，小明用到了两次平移一次旋转，你能用两次旋转一次平移复制形成一个四边形吗？如果能，请在图2的方框内画出草图，并仿照图1作出标记；如果不能，请说明理由；
    （4）图3是正五边形EFGHI，其中心是O，连接O点与各顶点．将其中的一个三角形记为△A，小明认为正五边形EFGHI是由复制形成的一种结果，你认为他的说法对吗？请判断并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网（1）求值：
    		8
    -8×
    1
    2
    +(-
    1
    2
    )-2    ，
    （2）在正方形方格纸中，我们把顶点都在“格点”上的三角形称为“格点三角形”，如图，△ABC是一个格点三角形．
    ①请你在所给的方格纸中，以O为位似中心，将△ABC放大为原来的2倍，得到一个△A1B1C1．
    ②若每一个方格的面积为1，则△A1B1C1的面积为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    写出下列事件发生的可能性，并标在图中的大致位置上．
    （1）袋中有10个红球，摸到红球；
    （2）袋中有10个红球，摸到白球；
    （3）从一副混合均匀的扑克牌中（除去大、小．从中任意抽取一张，这一张恰好是A；
    （4）一个布袋中有2个黑球和2个白球，从中任意摸出一个球，恰好是黑球；
    （5）任意掷出一个质地均匀的小立方体（每个面上分别标有数字1，2，3，4，5，6），朝上一面的数字大于2．

    查看答案和解析>>

    同步练习册答案