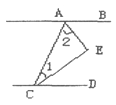
【题目】如图，已知AB∥CD，CE、AE分别平分
、
，则
= ( )
A.
B.
C.
D.
【答案】B
【解析】
由AB∥CD，根据两直线平行，同旁内角互补，可得∠BAC+∠ACD=180°，又由CE、AE分别平分∠ACD、∠CAB，可得
，
，则可求得∠1+∠2的度数．
∵AB∥CD，
∴∠BAC+∠ACD=180°，
∵CE、AE分别平分∠ACD、∠CAB，
∴，，
∴
．
故选B．
【考点精析】通过灵活运用平行线的性质和三角形的内角和外角，掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题．
导学全程练创优训练系列答案科目：初中数学 来源： 题型：
【题目】凤凰古城门票事件后，游客相比以往大幅减少，滨江某旅行社为吸引市民组团去旅游，推出了如下收费标准： 
某单位组织员工去凤凰古城旅游，共支付给该旅行社旅游费用27000元，请问该单位这次共有多少员工去凤凰古城旅游？
查看答案和解析>>
科目：初中数学 来源： 题型：
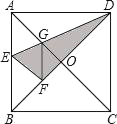
【题目】如图，在正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后，折痕DE分别交AB，AC于点E、G，连接GF，有下列结论：
①∠AGD=112.5°；②tan∠AED=
+1；③四边形AEFG是菱形；④S△ACD=
S△OCD．其中正确结论的序号是__．（把所有正确结论的序号都填在横线上）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（8分）为了贯彻落实市委市府提出的“精准扶贫”精神．某校特制定了一系列关于帮扶A、B两贫困村的计划．现决定从某地运送152箱鱼苗到A、B两村养殖，若用大小货车共15辆，则恰好能一次性运完这批鱼苗，已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆，其运往A、B两村的运费如下表：
（1）求这15辆车中大小货车各多少辆？
（2）现安排其中10辆货车前往A村，其余货车前往B村，设前往A村的大货车为x辆，前往A、B两村总费用为y元，试求出y与x的函数解析式．
（3）在（2）的条件下，若运往A村的鱼苗不少于100箱，请你写出使总费用最少的货车调配方案，并求出最少费用．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列式子中一定相等的是（ ）
A.（a﹣b）2=a2+b2
B.a2+b2=（a+b）2
C.（a﹣b）2=b2﹣2ab+a2
D.（a+b）（a2﹣ab+b2）=a3﹣b3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
