练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．如图是建筑大师梁思成先生所做的“清代北平西山碧云寺金刚宝座塔”手绘建筑图．1925年孙中山先生在北京病逝后，他的衣帽被封存于此塔内，因此也被称为“孙中山先生衣冠冢”．在图中所示的俯视图的示意图中建立如图所示的平面直角坐标系，其中的小正方形网格的宽度为1，那么图中塔的外围左 上角处点C的坐标是（-2，5）．

    分析 直接利用已知坐标系结合C点位置进而得出答案．

    解答 解：如图所示：可得C点坐标为：（-2，5）．
    故答案为：（-2，5）．

    点评 此题主要考查了坐标确定位置，正确利用坐标系得出C点位置是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    16．小强由甲地匀速步行到乙地后原路返回，小亮由甲地匀速步行经乙地到丙地后原路返回，两人同时出发，他们离乙地的路程S（km）与步行的时间t（h）间的函数关系如图所示，则下列说法中正确的个数有（　　）
    ①甲、乙两地之间的路程为8km
    ②乙、丙两地之间的路程为2km
    ③小亮的平均速度为10千米/时
    ④小强的平均速度为4km/时．
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列图形中，是中心对称图形的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，直线l1：y=-2x与直线l2：y=kx+b在同一平面直角坐标系内交于点P．
    （1）直接写出不等式-2x＞kx+b的解集x＜3；
    （2）设直线l2与x轴交于点A，△OAP的面积为12，求l2的表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．阅读下面材料：
    小伟遇到这样一个问题：如图1，在△ABC中，AB=AC，在边AB上取点E，在边AC上取点F，使BE=AF（E，F不是AB，AC边的中点），连结EF．求证：EF＞$\frac{1}{2}$BC．
     
    小伟是这样思考的：要想解决这个问题，首先应想办法移动这些分散的线段，构造全等三角形，再证明线段的关系．他先后尝试了翻折，旋转，平移的方法，发现通过平移可以解决这个问题．他的方法是过点C作CH∥BE，并截取CH=BE，连接EH，构造出平行四边形EBCH，再连接FH，进而证明△AEF≌△CFH，得到FE=FH，使问题得以解决（如图2）．
    （1）请回答：在证明△AEF≌△CFH时，CH=AF，∠HCF=∠A．
    （2）参考小伟思考问题的方法，解决问题：
    如图3，△ABC中，∠BAC=90°，AB=AC，延长CA到点D，延长AB到点E，使AD=BE，∠DEA=15°．
    判断DE与BC的数量关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，在平面直角坐标系中，过点A（2，0）的直线l与y轴交于点B，tan∠OAB=$\frac{1}{2}$，直线l上的点P位于y轴左侧，且到y轴的距离为1．
    （1）求直线l的表达式；
    （2）若反比例函数y=$\frac{m}{x}$的图象经过点P，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

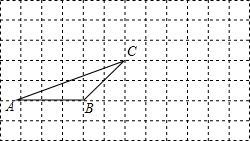    5．如图：在正方形网格中有一个格点三角形ABC，（即△ABC的各顶点都在格点上），按要求进行下列作图：
    （1）画出△ABC中AB边上的高CD；（提醒：别忘了标注字母！）
    （2）画出将△ABC先向右平移5格，再向上平移3格后的△A′B′C′；
    （3）画一个锐角格点三角形MNP，使其面积等于△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，Rt△ABC中，∠C=90°，∠CAB=37°，AB=5，AC=4，BC=3，直线MN经过点C，交边AB于点D，分别过点A，B作AF⊥MN，BE⊥MN，垂足分别为点E，F，设线段BE，AF的长度分别为d1，d2．
    （1）求△ABC的面积；
    （2）若直线MN从与CB重合位置开始顺时针绕着点C旋转，至与CA重合时停止，在旋转过程中，试求出d1+d2的最大值，并求出此时直线MN旋转角的度数（即∠BCD的度数）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知：如图，在8×12的矩形网格中，每个小正方形的边长都为1，四边形ABCD的顶点都在格点上．
    （1）以B为坐标原点，AB所在直线为x轴，建立直角坐标系；
    （2）写出四边形各顶点的坐标；
    （3）计算四边形的面积；
    （4）画出将四边形向右平移5个单位，向下平移2个单位得到的图形．

    查看答案和解析>>

    同步练习册答案