

分析 (1)利用描点法画y=|x|的图象;
(2)根据绝对值的意义,利用分类讨论的思想写出分段函数;
(3)与(2)画函数图象的方法一样,把函数y=x2-2x-3的图象在x轴下面部分,沿x轴进行翻折可得到函数y=|x2-2x-3|的图象;
(4)利用画函数图象,通过确定y=|x2-2x-3|的图象与直线y=a的交点个数解决问题.
解答 解:(1)操作发现
如图1,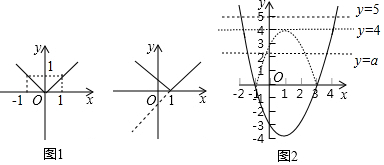
(2)类比探究
作函数y=|x-1|的图象,可以转化为分段函数y=$\left\{\begin{array}{l}{x-1(x≥1)}\\{-x+1(x<1)}\end{array}\right.$;
(3)拓展提高
把函数y=x2-2x-3的图象在x轴下面部分,沿x轴进行翻折,与x轴上及上面部分组成了函数y=|x2-2x-3|的图象,如图2右图;
(4)实际运用
1)函数y=|x2-2x-3|的图象与x轴有 2个交点,对应方程|x2-2x-3|=0有2个实根;
2)函数y=|x2-2x-3|的图象与直线y=5有 2个交点,对应方程|x2-2x-3|=5有2个实根;
3)函数y=|x2-2x-3|的图象与直线y=4有3个交点,对应方程|x2-2x-3|=4有3个实根;
4)关于x的方程|x2-2x-3|=a有4个实根时,a的取值范围是 0<a<4.
故答案为y=$\left\{\begin{array}{l}{x-1(x≥1)}\\{-x+1(x<1)}\end{array}\right.$;2,2;2,2;3,3;0<a<4.
点评 本题考查了几何变换综合题:熟练掌握折叠的性质、一次函数和二次函数的性质;会利用分类讨论的方法解决绝对值函数;会利用数形结合的思想,把求方程的解的个数问题转化为两函数的交点个数问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com