
 如图,AP⊥AQ,半径为5 的⊙O于AP相切于点T,与AQ交于点B、C.
如图,AP⊥AQ,半径为5 的⊙O于AP相切于点T,与AQ交于点B、C.分析 ①连接OT,AT是切线,则OT⊥AP,可以证明AB∥OT,得到∠TBA=∠BTO,再根据等边对等角得到∠OTB=∠OBT,就可以证出结论;
②过点B作BH⊥OT于点H,然后在Rt△OBH中,利用OB=5,BH=AT=4根据勾股定理求出OH,最后即可求出AB.
解答 解:①BT平分∠OBA,
证明:连接OT,
∵AT是切线,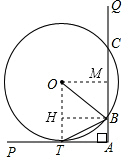
∴OT⊥AP;
又∵∠PAB是直角,即AQ⊥AP,
∴AB∥OT,
∴∠TBA=∠BTO.
又∵OT=OB,
∴∠OTB=∠OBT.
∴∠OBT=∠TBA,即BT平分∠OBA;
②过点B作BH⊥OT于点H,
则四边形OMBH和四边形ABHT都是矩形.
则在Rt△OBH中,OB=5,BH=AT=4,
∴OH=$\sqrt{O{B}^{2}-B{H}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴AB=HT=OT-OH=5-3=2.
点评 此题考查了切线的性质,勾股定理,等腰三角形的性质,平行线的判定与性质,及垂径定理,熟练掌握切线的性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
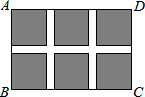 如图,某小区规划在一个长30m、宽20m的长方形ABCD土地上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2,那么通道的宽应设计成多少m?设通道的宽为xm,由题意列得方程x2-35x+66=0.
如图,某小区规划在一个长30m、宽20m的长方形ABCD土地上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2,那么通道的宽应设计成多少m?设通道的宽为xm,由题意列得方程x2-35x+66=0.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
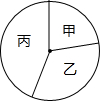 如图,将一个圆分割成甲、乙、丙三个扇形,使它们的圆心角的度数之比为2:3:4.若圆的半径为3,则扇形丙的面积为( )
如图,将一个圆分割成甲、乙、丙三个扇形,使它们的圆心角的度数之比为2:3:4.若圆的半径为3,则扇形丙的面积为( )| A. | $\frac{2}{3}$π | B. | $\frac{4}{9}$π | C. | 3π | D. | 4π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等边△ABC的边长为2,P是BC边上的任一点(与B、C不重合),设BP=x,连接AP,以AP为边向两侧作等边△APD和等边△APE,分别与边AB、AC交于点M、N.
如图,等边△ABC的边长为2,P是BC边上的任一点(与B、C不重合),设BP=x,连接AP,以AP为边向两侧作等边△APD和等边△APE,分别与边AB、AC交于点M、N.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,AC,BD交于点O,OE⊥BD,交AD边于点E,若?ABCD的周长为20,则△ABE的周长为( )
如图,在?ABCD中,AC,BD交于点O,OE⊥BD,交AD边于点E,若?ABCD的周长为20,则△ABE的周长为( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com