

分析 (1)a分钟新增4a人,两个窗口售出2×3a份饭,此时窗口有240人,据此得方程求解;
(2)运用待定系数法求直线解析式,求x=60时的函数值;
(3)根据题意列不等式求解.
解答 解:(1)由图①②可知,每分钟新增购饭人数4人,每个售饭窗口每分钟售饭3人,则:
300+4a-3×2a=240
解这个方程,得a=30;
(2)设第30-78分钟时,餐厅排队等候售饭的人数y与售饭时间x的函数关系式y=kx+b(k≠0),
则30k+b=240;78k+b=0.
解得k=-5,b=390.
∴y=-5x+390.
当x=60时,y=-5×60+390=90.
因此,售饭到第60分钟时,餐厅排队等候购饭有90人;
(3)设需同时开放n个售饭窗口,依题意得:
300+30×4≤30×3×n,
解得n≥$\frac{14}{3}$,
因此至少同时开放5个售饭窗口.
点评 此题主要考查了一次函数的应用,是函数与实际问题的综合应用大题,要注意函数图象的运用及方程、不等式的联合运用.


科目:初中数学 来源: 题型:解答题
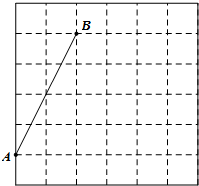 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在所有连结两点的线中,直线最短 | |
| B. | ∠AOB与∠BOA表示相同的角 | |
| C. | 一个锐角与一个钝角的和是一个平角 | |
| D. | 两点之间的线段是两点之间的距离 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com