

分析 (1)由等腰直角三角形的性质得到AP=BP=$\frac{\sqrt{2}}{2}$AB=4,根据三角形中位线的性质,得到EF∥AB,EF=$\frac{1}{2}$AB=2$\sqrt{2}$,再由勾股定理得到结果;
(2)连接EF,设∠ABP=α,类比着(1)即可证得结论;
(3)根据全等三角形的性质得到BG=EG,AG=GF,得到BG是△ABF的中线,取AB的中点H,连接FH,并延长交DA的延长线于P,推出四边形CSPF是平行四边形,根据平行四边形的性质得到FP∥CE,得到△ABF是中垂三角形,于是得到结论.
解答 解:(1)∵AF⊥BE,∠ABE=45°,
∴AP=BP=$\frac{\sqrt{2}}{2}$AB=4,
∵AF,BE是△ABC的中线,
∴EF∥AB,EF=$\frac{1}{2}$AB=2$\sqrt{2}$,
∴∠PFE=∠PEF=45°,
∴PE=PF=2,
在Rt△FPB和Rt△PEA中,
AE=BF=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,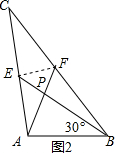
∴AC=BC=4$\sqrt{5}$,
∴a=b=4$\sqrt{5}$,
如图2,连接EF,
同理可得:EF=$\frac{1}{2}$×2=1,
∵EF∥AB,
∴△PEF~△ABP,
∴$\frac{FP}{AP}$=$\frac{PE}{PB}$,
在Rt△ABP中,
AB=2,∠ABP=30°,
∴AP=1,PB=$\sqrt{3}$,
∴PF=$\frac{1}{2}$,PE=$\frac{\sqrt{3}}{2}$,
在Rt△APE和Rt△BPF中,
AE=$\frac{\sqrt{7}}{2}$,BF=$\frac{\sqrt{13}}{2}$,
∴a=$\sqrt{13}$,b=$\sqrt{7}$,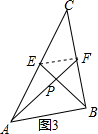
故答案为:4$\sqrt{5}$,4$\sqrt{5}$,$\sqrt{13}$,$\sqrt{7}$;
(2)猜想:a 2,b2,c2三者之间的关系是:a2+b2=5c2,
证明:如图3,连接EF,∵AF,BE是△ABC的中线,
∴EF是△ABC的中位线,
∴EF∥AB.且 EF=$\frac{1}{2}$AB=$\frac{1}{2}$c.
∴$\frac{PE}{PB}$=$\frac{PF}{PA}$=$\frac{1}{2}$,
设 PF=m,PE=n 则AP=2m,PB=2n,
在Rt△APB中,(2m)2+(2n)2=c2①
在Rt△APE中,(2m)2+n2=($\frac{b}{2}$)2 ②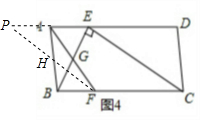
在Rt△BPF中,m2+(2n)2=($\frac{a}{2}$)2 ③
由①得:m2+n2=$\frac{{c}^{2}}{4}$,由②+③得:5( m2+n2)=$\frac{{a}^{2}+{b}^{2}}{4}$,
∴a 2+b2=5 c2;
(3)在△AGE与△FGB中,$\left\{\begin{array}{l}{∠AGE=∠FGB}\\{∠AEG=∠FBG}\\{AE=BF}\end{array}\right.$,
∴△AGE≌△FGB,
∴BG=EG,AG=GF,
∴BG是△ABF的中线,
取AB的中点H,连接FH,并延长交DA的延长线于P,
同理,△APH≌△BFH,
∴AP=BF,PE=CF=2BF,
∴PE∥CF,PE=CF,
∴四边形CSPF是平行四边形,
∴FP∥CE,
∵BE⊥CE,
∴FP⊥BE,即FH⊥BG,
∴△ABF是中垂三角形,
由(2)知,AB2+AF2=5BF2,
∵AB=3,
∴BF=$\frac{1}{3}$AD=$\sqrt{5}$.
点评 此题主要考查了等腰三角形的性质和判定,勾股定理,三角形的中位线,表示出线段是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
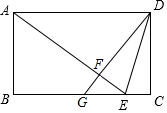 如图,矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE于点F,延长DF交BC于点G,连接DE.
如图,矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE于点F,延长DF交BC于点G,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
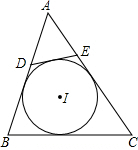 如图,⊙I为△ABC的内切圆,D、E分别为边AB、AC上的点,且DE为⊙I的切线,若△ABC的周长为19,BC边的长为5,则△ADE的周长为9.
如图,⊙I为△ABC的内切圆,D、E分别为边AB、AC上的点,且DE为⊙I的切线,若△ABC的周长为19,BC边的长为5,则△ADE的周长为9.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是40cm.
如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是40cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 3 | B. | 4 | C. | 6 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
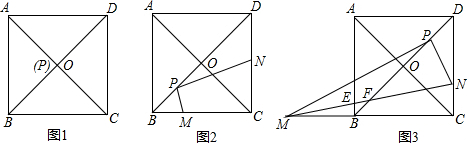
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 平均数 | 中位数 | 方差 | 命中10环的次数 | |
| 甲 | 7 | 7 | 4 | 0 |
| 乙 | 7 | 7.5 | 5.4 | 1 |
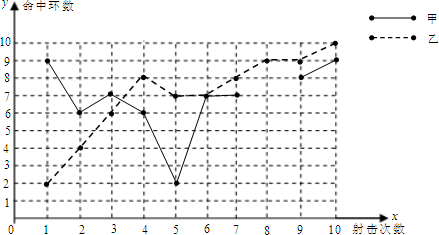
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com