
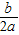 ,顶点坐标为(-
,顶点坐标为(- ,
, ),与x轴的交点的纵坐标为0.
),与x轴的交点的纵坐标为0. ,x2=
,x2=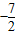 ,
, ,0),(
,0),(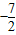 ,0);
,0); ,
, ;
; ,顶点坐标是
,顶点坐标是 ,
,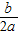 ,顶点坐标为(-
,顶点坐标为(- ,
, ),与x轴的交点的纵坐标为0.
),与x轴的交点的纵坐标为0. 

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
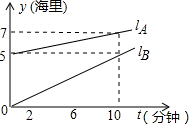 、lB分别表示y2、y1与t之间的关系.结合图象回答下列问题:
、lB分别表示y2、y1与t之间的关系.结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
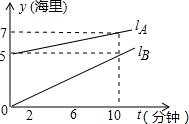 、lB分别表示y2、y1与t之间的关系.结合图象回答下列问题:
、lB分别表示y2、y1与t之间的关系.结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
我国青海省玉树地区发生强烈地震以后,国家立即启动救灾预案,积极展开灾区运送救灾物资和对伤员的救治工作.已知西宁机场和玉树机场相距800千米,
乙两机沿同一航线各自从西宁、玉树出发,相向而行.如图,线段AB、CD分别表示甲、乙
两机离玉树机场的距离S(百千米)和所用去的时间t(小时)之间的函数关系的图象(注:
为了方便计算,将平面直角坐标系中距离S的单位定为(百千米)).观察图象回答下列问题:
(1)乙机在甲机出发后几小时,才从玉树机场出发?甲、乙两机的飞行速度每小时各为多少千米?
(2)求甲、乙两机各自的S与t的函数关系式;
(3)甲、乙两机相遇时,乙机飞行了几小时?离西宁机场多少千米?
查看答案和解析>>
科目:初中数学 来源:2004年湖北省荆州市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(江苏常州) 题型:解答题
我国青海省玉树地区发生强烈地震以后,国家立即启动救灾预案,积极展开灾区运送救灾物资和对伤员的救治工作.已知西宁机场和玉树机场相距800千米,
乙两机沿同一航线各自从西宁、玉树出发,相向而行.如图,线段AB、CD分别表示甲、乙
两机离玉树机场的距离S(百千米)和所用去的时间t(小时)之间的函数关系的图象(注:
为了方便计算,将平面直角坐标系中距离S的单位定为(百千米)).观察图象回答下列问题:
(1)乙机在甲机出发后几小时,才从玉树机场出发?甲、乙两机的飞行速度每小时各为多少千米?
(2)求甲、乙两机各自的S与t的函数关系式;
(3)甲、乙两机相遇时,乙机飞行了几小时?离西宁机场多少千米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com