

 ����2����
����2���� ��0������3���ٲ����ڣ����ɼ������������
��0������3���ٲ����ڣ����ɼ������������ ����
���� ��
�� ʱ����ʱS=
ʱ����ʱS= OE•OD���ɴ˿ɵó�����S��t�ĺ�����ϵʽ��
OE•OD���ɴ˿ɵó�����S��t�ĺ�����ϵʽ�� ʱ����ʱS=
ʱ����ʱS= OD��E��������꣮�ɴ˿ɵó�����S��t�ĺ�����ϵʽ��
OD��E��������꣮�ɴ˿ɵó�����S��t�ĺ�����ϵʽ�� ����ʱ�õ�ʱ�䣬��ʱS=S��AOE��S��AOD���ɴ˿ɵó�S��t�ĺ�����ϵʽ��
����ʱ�õ�ʱ�䣬��ʱS=S��AOE��S��AOD���ɴ˿ɵó�S��t�ĺ�����ϵʽ�� ����ͼ����㣨0����8������
����ͼ����㣨0����8������ ������κ����Ľ���ʽΪ
������κ����Ľ���ʽΪ ��
�� =
= �����M��������2��
�����M������Ϊ��2�� �����ߵ�C������Ϊ��0��
�����ߵ�C������Ϊ��0�� �������C����x��ԳƵĵ�C�������Ϊ��0��8������ֱ��C��M�Ľ���ʽΪ��
�������C����x��ԳƵĵ�C�������Ϊ��0��8������ֱ��C��M�Ľ���ʽΪ�� ����
���� ����
���� ����ã�
����ã� �����K������Ϊ��
�����K�������� ��0����
��0���� ����PQ��OC�����APQ�ס�AOC����
����PQ��OC�����APQ�ס�AOC���� ����AP=
����AP= ��AQ=
��AQ= ����
���� ����
���� ����
���� ��2������
��2������ �������PQ��OC��
�������PQ��OC��

 OP•OQ=
OP•OQ= ��
��
 OP•EQ=
OP•EQ= ��
�� ��
�� ��S=
��S= QP•OF=
QP•OF= ��
�� ��
�� ʱ��
ʱ�� �����������ֵ��12��
�����������ֵ��12�� ʱ��
ʱ�� �����������ֵ��
�����������ֵ�� ��
�� ��
�� �����������ֵΪ
�����������ֵΪ ��
�� ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
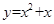 ����ƽ��2����λ������ƽ��3����λ�����������ߵı���ʽ�� ��
����ƽ��2����λ������ƽ��3����λ�����������ߵı���ʽ�� ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ����O��D��C���㣮
����O��D��C���㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ��x�ύ��A��B���㣬��y�ύ��C�㣬�ı���OBHCΪ���Σ�CH���ӳ��߽��������ڵ�D��5��2��������BC��AD.
��x�ύ��A��B���㣬��y�ύ��C�㣬�ı���OBHCΪ���Σ�CH���ӳ��߽��������ڵ�D��5��2��������BC��AD.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
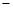 2��4) �͵�B (1��0)����������
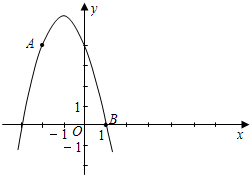
2��4) �͵�B (1��0)����������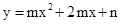 ��.
��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
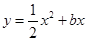 ��ֱ��
��ֱ��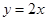 ���ڵ�
���ڵ�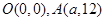 ����
����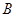 ����������
����������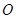 ��
��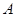 ֮���һ�����㣬����
֮���һ�����㣬����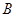 �ֱ���
�ֱ���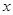 �ᡢ
�ᡢ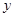 ���ƽ������ֱ��
���ƽ������ֱ��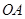 ���ڵ�
���ڵ�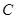 ��
��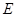 ��
��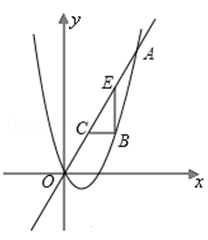
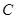 �ĺ�����Ϊ2����
�ĺ�����Ϊ2����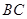 �ij���
�ij���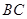 ��
��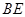 Ϊ�߹������
Ϊ�߹������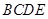 �����
�����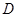 ������Ϊ
������Ϊ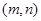 �����
�����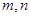 ֮��Ĺ�ϵʽ��
֮��Ĺ�ϵʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A��x1��x2��a��b | B��x1��a��x2��b | C��x1��a��b��x2 | D��a��x1��b��x2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��

 B��
B�� C��
C�� D��
D��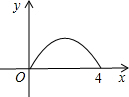
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com