
【题目】如图,在△ABC中,∠ACB=90,CD⊥AB,BC=1.
(1)如果∠BCD=30,求AC;
(2)如果tan∠BCD=![]() ,求CD.
,求CD.

【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】(1)根据直角三角形的两锐角互余,由∠BCD的度数求出∠B的度数,利用锐角三角函数定义表示出tanB,将tanB及BC的长代入,即可求出AC的长;
(2)在直角三角形BDC中,由已知tan∠BCD的值,利用锐角三角函数定义得出BD与CD的比值为1:3,根据比值设出BD=k,CD=3k,再由BC的长,利用勾股定理列出关于k的方程,求出方程的解得到k的值,即可求出CD的长.
解:(1)∵CD⊥AB,∴∠BDC=90°.
∵∠DCB=30°,∴∠B=60°.
在Rt△ACB中,∠ACB=90°,∴tan60°=![]() .
.
∵BC=1,∴![]() ,则AC=
,则AC=![]() .
.
(2)在Rt△BDC中,tan∠BCD=![]() .
.
设BD=k,则CD=3k,
又BC=1,由勾股定理得:k2+(3k)2=1,解得:k=![]() 或k=
或k= ![]() (舍去).
(舍去).
∴CD=3k=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在半径为27m的广场中央,点O的上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°(如图),求光源离地面的垂直高度SO.(精确到0.1m;![]() =1.44,
=1.44,![]() =1.732,
=1.732,![]() =2.236,以上数据供参考)
=2.236,以上数据供参考)

查看答案和解析>>
科目:初中数学 来源: 题型:
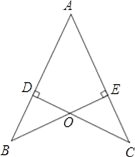
【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证:AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.

(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点C距守门员多少米?(取![]() )
)
(3)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,已知1克=1000毫克,那么0.000000037毫克可用科学记数法表示为( )
A.3.7×10﹣5克
B.3.7×10﹣6克
C.37×10﹣7克
D.3.7×10﹣8克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列说法中,正确的是( )
A. 任何等腰三角形的顶角都大于底角
B. 关于某直线成轴对称的两个三角形全等
C. 等腰三角形的对称轴是底边中线
D. 等边三角形只有一条对称轴
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com