
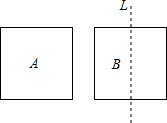
 操作:有2张边长都是2的正方形纸片A和B,请你将纸片A的一边的一个端点放在纸片B的对称轴L上,另一个端点与纸片B的一个顶点重合后压平.求纸片A与纸片B重合部分的面积.
操作:有2张边长都是2的正方形纸片A和B,请你将纸片A的一边的一个端点放在纸片B的对称轴L上,另一个端点与纸片B的一个顶点重合后压平.求纸片A与纸片B重合部分的面积. 分析 如图,设纸片A与纸片B重合部分为四边形EFGH或四边形GFNM,根据已知条件得:EF=FG=FN=2,∠E=∠FGH=∠N=∠FGM=∠P=90°,证得Rt△EFH≌Rt△FGH,得到HG=EH,同理可证Rt△FGM≌Rt△FNM,得到GM=NM,设GM=NM=x,HG=EH=y,则PM=2-x,PH=2-y,HM=x+y,在Rt△PHM中,HM2=PH2+PM2,即(x+y)2=(2-x)2+(2-y)2 ①,根据相似三角形的性质得到$\frac{1}{2-x}=\frac{2}{x+y}$,于是得到y=-3x+4 ②,把②代入①,求出MN=$\frac{2\sqrt{3}}{3}$,EH=4-2$\sqrt{3}$,即可得到结果.
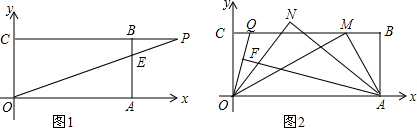
解答  解:如图,设纸片A与纸片B重合部分为:四边形EFGH或四边形GFNM,
解:如图,设纸片A与纸片B重合部分为:四边形EFGH或四边形GFNM,
根据已知条件得:EF=FG=FN=2,∠E=∠FGH=∠N=∠FGM=∠P=90°,
在Rt△EFH与Rt△FGH中,
$\left\{\begin{array}{l}{EF=FG}\\{FH=FH}\end{array}\right.$,
∴Rt△EFH≌Rt△FGH,
∴HG=EH,
同理Rt△FGM≌Rt△FNM,
∴GM=NM,
设GM=NM=x,HG=EH=y,则PM=2-x,PH=2-y,HM=x+y,
在Rt△PHM中,HM2=PH2+PM2,
即(x+y)2=(2-x)2+(2-y)2 ①,
∵∠GFQ=∠PMH=180°-∠HMN,∠FQG=∠FGM=90°,
∴△FQG∽△HPM,
∴$\frac{FQ}{PM}=\frac{FG}{HM}$,
∴$\frac{1}{2-x}=\frac{2}{x+y}$,
∴y=-3x+4 ②,
把②代入①,解得:x=$\frac{2\sqrt{3}}{3}$,y=4-2$\sqrt{3}$,
∴MN=$\frac{2\sqrt{3}}{3}$,EH=4-2$\sqrt{3}$,
∴四边形EFGH的面积=2×$\frac{1}{2}×2×(4-2\sqrt{3})$=8-4$\sqrt{3}$,
四边形GFNM面积=2×$\frac{1}{2}×2×\frac{2\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$,
∴纸片A与纸片B重合部分为:8-4$\sqrt{3}$,$\frac{4\sqrt{3}}{3}$.
点评 本题考查了翻折变换-折叠问题,正方形的性质,三角形面积的求法,相似三角形的判定和性质,正确的画出图形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠3是它的一个外角,E为边AC上一点,D在BC的延长上,则∠1、∠2、∠3之间的关系是( )
如图,在△ABC中,∠3是它的一个外角,E为边AC上一点,D在BC的延长上,则∠1、∠2、∠3之间的关系是( )| A. | ∠3>∠2>∠1 | B. | ∠2>∠3>∠1 | C. | ∠3=∠1+∠2 | D. | ∠1+∠2+∠3=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
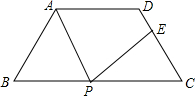 如图,在等腰梯形ABCD中,AD∥BC,AD=6cm,BC=14cm,∠B=60°,P为下底BC上一点(不与点B、C重合),连接AP,过点P作射线PE交线段DC于点E,使得∠APE=∠B,若DE:EC=5:3,则BP=2cm或12cm.
如图,在等腰梯形ABCD中,AD∥BC,AD=6cm,BC=14cm,∠B=60°,P为下底BC上一点(不与点B、C重合),连接AP,过点P作射线PE交线段DC于点E,使得∠APE=∠B,若DE:EC=5:3,则BP=2cm或12cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com