
 ,那么△ABC是( )
,那么△ABC是( )| A.钝角三角形; | B.直角三角形; | C.锐角三角形; | D.等腰三角形 |
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 课题 | 测量教学楼高度 | |
| 方案 | 一 | 二 |
| 图示 |  |  |
| 测得数据 | CD=6.9m,∠ACG=22°,∠BCG=13°, | EF=10m,∠AEB=32°,∠AFB=43° |
| 参考数据 | sin22°≈0.37,cos22°≈0.93, tan22°≈0.40 sin13°≈0.22,cos13°≈0.97 tan13°≈0.23 | sin32°≈0.53,cos32°≈0.85,tan32°≈0.62 sin43°≈0.68,cos43°≈0.73,tan43°≈0.93 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

 ; (B)
; (B) ; (C)
; (C) ; (D)60米。
; (D)60米。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
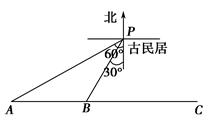
 处有一热气球,以每分钟
处有一热气球,以每分钟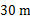 的速度沿着仰角为60°的方向上升,20 min后升到
的速度沿着仰角为60°的方向上升,20 min后升到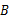 处,这时热气球上的人发现在
处,这时热气球上的人发现在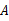 的正西方向俯角为45°的
的正西方向俯角为45°的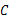 处有一着火点,求热气球的升空点
处有一着火点,求热气球的升空点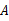 与着火点
与着火点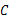 的距离(结果保留根号).
的距离(结果保留根号).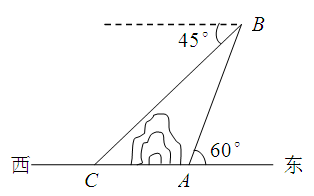
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com