
分析 据完全平方和公式展开(a+b+c)2,然后将a+b+c=0,a2+b2+c2=1整体代入来求ab+bc+ca的值;根据完全平方和公式展开(a+b+c)4,然后将a+b+c=0,ab+bc+ca=-2整体代入来求a4+b4+c4的值.
解答 解:∵a+b+c=0,
∴(a+b+c)2=0,即a2+b2+c2+2ab+2bc+2ca=0,
∴a2+b2+c2+2(ab+bc+ca)=0,①
∵a2+b2+c2=4,②
把②代入①,得
4+2(ab+bc+ca)=0,
解得,ab+bc+ca=-2;
∵a4+b4+c4=(a2+b2+c2)2-2(a2b2+b2c2+c2a2)=(a2+b2+c2)2-2[(ab+bc+ac)2-2abc(a+b+c)],
ab+bc+ca=-2,a+b+c=0,
∴a4+b4+c4
=16-2×[(-2)2-0]
=8.
故答案为:8.
点评 本题考查了完全平方公式,难度较大,关键是正确利用条件变形为完全平方的形式,再进行求解.


科目:初中数学 来源: 题型:解答题
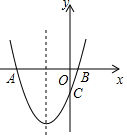 如图,抛物线y=x2+2x+k+1与x轴交与A、B两点,与y轴交与点C(0,-3).
如图,抛物线y=x2+2x+k+1与x轴交与A、B两点,与y轴交与点C(0,-3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 设△ABC中BC边的长为x(cm),BC上的高线AD为y(cm),现一探究小组测得两个变量x(x>0),y(y>0)的一组对应值如表:
设△ABC中BC边的长为x(cm),BC上的高线AD为y(cm),现一探究小组测得两个变量x(x>0),y(y>0)的一组对应值如表:| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 6 | 2.9 | 2.1 | 1.5 | 1.2 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com