练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在矩形ABCD中，AB＝5，AD＝3，动点P满足S△PAB＝S矩形ABCD，则点P到A、B两点距离之和PA+PB的最小值为_____．

    【答案】

    【解析】

    已知S△PAB＝S矩形ABCD ，则可以求出△ABP的高，此题为“将军饮马”模型，过P点作直线l∥AB，作点A关于l的对称点E，连接AE，连接BE，则BE的长就是所求的最短距离.

    解：设△ABP中AB边上的高是h．

    ∵S△PAB＝S矩形ABCD，

    ∴ABh＝ABAD，

    ∴h＝AD＝2，

    ∴动点P在与AB平行且与AB的距离是2的直线l上，如图，作A关于直线l的对称点E，连接AE，连接BE，则BE的长就是所求的最短距离．

    在Rt△ABE中，∵AB＝5，AE＝2+2＝4，

    ∴BE＝，

    即PA+PB的最小值为．

    故答案为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，△OA1B1，△A1A2B2，△A2A3B3，…是分别以A1，A2，A3，…为直角顶点，一条直角边在x轴正半轴上的等腰直角三角形，其斜边的中点C1（x1，y1），C2（x2，y2），C3（x3，y3），…均在反比例函数（x＞0）的图象上．则y1+y2+…+y8的值为（ ）

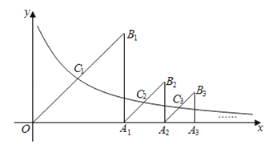
    A.B.6C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

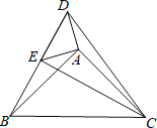
    【题目】 如图，点E在△DBC的边DB上，点A在△DBC内部，∠DAE=∠BAC=90°，AD=AE，AB=AC．给出下列结论：①BD=CE；②BC=DC；③∠ABD+∠ECB=45°；④BD⊥CE．其中正确的结论是（　　）

    A.①②③④B.②④C.①②③D.①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】初一（1）班针对“你最喜爱的课外活动项目”对全班学生进行调查（每名学生分别选一个活动项目），并根据调查结果列出统计表，绘制成扇形统计图．

    男、女生所选项目人数统计表

    项目

    男生（人数）

    女生（人数）

    机器人

    7

    9

    3D打印

    m

    4

    航模

    2

    2

    其他

    5

    n

    根据以上信息解决下列问题：

    （1）m＝　 　，n＝　 　；

    （2）扇形统计图中机器人项目所对应扇形的圆心角度数为　 　°；

    （3）从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练，请用列举法（画树状图或列表）求所选取的2名学生中恰好有1名男生、1名女生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，AO是的半径，AC为的弦，点F为的中点，OF交AC于点E，AC=8，EF=2．

    （1）求AO的长；

    （2）过点C作CD⊥AO，交AO延长线于点D，求sin∠ACD的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AB＝AC，以AB为直径的⊙O与BC相交于点D，与CA的延长线相交于点E，过点D作DF⊥AC于点F．

    （1）证明：DF是⊙O的切线；

    （2）若AC＝3AE，FC＝6，求AF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“大千故里，文化内江”，我市某中学为传承大千艺术精神，征集学生书画作品．王老师从全校20个班中随机抽取了4个班，对征集作品进行了数量分析统计，绘制了如下两幅不完整的统计图．

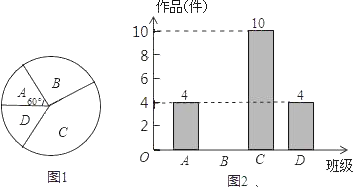
    （1）王老师采取的调查方式是　 　（填“普查”或“抽样调査”），王老师所调查的4个班共征集到作品　 　 件，并补全条形统计图；

    （2）在扇形统计图中，表示班的扇形周心角的度数为　 　；

    （3）如果全校参展作品中有4件获得一等奖，其中有1名作者是男生，3名作者是女生．现要从获得一等奖的作者中随机抽取两人去参加学校的总结表彰座谈会，求恰好抽中一男一女的概率．（要求用树状图或列表法写出分析过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为_____．

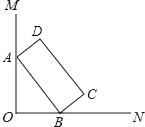
    查看答案和解析>>

    科目：初中数学 来源： 题型：

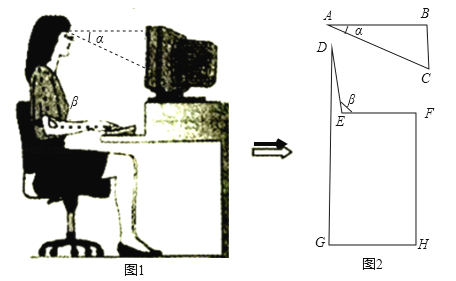
    【题目】（2017江西省）如图1，研究发现，科学使用电脑时，望向荧光屏幕画面的“视线角”α约为20°，而当手指接触键盘时，肘部形成的“手肘角”β约为100°．图2是其侧面简化示意图，其中视线AB水平，且与屏幕BC垂直．

    （1）若屏幕上下宽BC=20cm，科学使用电脑时，求眼睛与屏幕的最短距离AB的长；

    （2）若肩膀到水平地面的距离DG=100cm，上臂DE=30cm，下臂EF水平放置在键盘上，其到地面的距离FH=72cm．请判断此时β是否符合科学要求的100°？

    （参考数据：sin69°≈，cos21°≈，tan20°≈，tan43°≈，所有结果精确到个位）

    查看答案和解析>>

    同步练习册答案