
【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
(进价、售价均保持不变,利润 = 销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;

(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
【答案】(1)A、B两种型号电风扇的销售单价分别为250元、210元;(2)超市最多采购A种型号电风扇10台时,采购金额不多于5400元;(3)超市不能实现利润1400元的目标;
【解析】
(1)根据第一周和第二周的销售量和销售收入,可列写2个等式方程,再求解二元一次方程组即可;
(2)利用不多于5400元这个量,列写不等式,得到A型电风扇a台的一个取值范围,从而得出a的最大值;
(3)将B型电风扇用(30-a)表示出来,列写A、B两型电风扇利润为1400的等式方程,可求得a的值,最后在判断求解的值是否满足(2)中a的取值范围即可
解:(1)设A、B两种型号电风扇的销售单价分别为x元、y元,
依题意得:![]() ,解得:
,解得:![]() ,
,
答:A、B两种型号电风扇的销售单价分别为250元、210元.
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(30-a)台.
依题意得:200a+170(30-a)≤5400,解得:a≤10.
答:超市最多采购A种型号电风扇10台时,采购金额不多于5400元;
(3)依题意有:(250-200)a+(210-170)(30-a)=1400,
解得:a=20,∵a≤10,
∴在(2)的条件下超市不能实现利润1400元的目标.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】(2015攀枝花)某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元.
(1)若该超市一次性购进两种商品共80件,且恰好用去1600元,问购进甲、乙两种商品各多少件?
(2)若该超市要使两种商品共80件的购进费用不超过1640元,且总利润(利润=售价﹣进价)不少于600元.请你帮助该超市设计相应的进货方案,并指出使该超市利润最大的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中第九卷《勾股》主要讲述了以测量问题为中心的直角三角形三边互求,之中记载了一道有趣的“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”
译文:“今有正方形水池边长为1丈,有棵芦苇生长在它长出水面的部分为1尺.将芦苇的中央,向池岸牵引,恰好与水岸齐接.问水深,芦苇的长度分别是多少尺?”(备注:1丈=10尺)
如果设水深为![]() 尺,那么芦苇长用含
尺,那么芦苇长用含![]() 的代数式可表示为_______尺,根据题意,可列方程为______________.
的代数式可表示为_______尺,根据题意,可列方程为______________.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了分析九年级学生艺术考试的成绩,随机抽查了两个班级的各5名学生的成绩,它们分别是:
九(1)班:96,92,94,97,96
九(2)班:90,98,97,98,92
通过数据分析,列表如下:

(1)![]()
(2)计算两个班级所抽取的学生艺术成绩的方差,判断哪个班学生艺术成绩比较稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,∠XOY=90°,点A、B分别在射线OX、OY上移动,BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.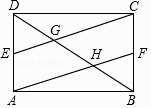
求证:
(1)四边形AFCE是平行四边形;
(2)证明:EG=FH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知在平面直角坐标系中,△ABC的位置如图所示:
(1)请写出点A、B、C三点的坐标.
(2)将△ABC向右平移6个单位,再向上平移2个单位,请在图中作出平移后的△A'B'C',并写出它们的坐标:A'( ),B'( ),C'( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com