
【题目】如图,图1中小正方形的个数为1个;图2中小正方形的个数为:1+3=4=22个;图3中小正方形的个数为:1+3+5=9=32个;图4中小正方形的个数为:1+3+5+7=16=42个;…
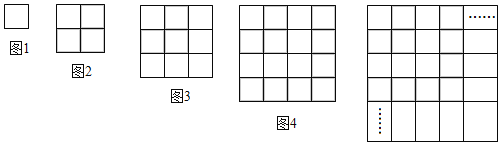
(1)根据你的发现,第n个图形中有小正方形:1+3+5+7+…+ = 个.
(2)由(1)的结论,解答下列问题:已知连续奇数的和:(2n+1)+(2n+3)+(2n+5)+……+137+139=3300,求n的值.
【答案】(1)(2n﹣1);n2;(2)n的值为40.
【解析】
(1)根据各图形中小正方形个数的变化可找出变化规律“第n个图形中有小正方形的个数为:1+3+5+7+…+(2n-1)=n2个”,此问得解;
(2)根据(1)的结论结合(2n+1)+(2n+3)+(2n+5)+……+137+139=3300,即可得出关于n的一元二次方程,解之取其正值即可得出结论.
解:(1)∵图1中小正方形的个数为1个;图2中小正方形的个数为:1+3=4=22个;图3中小正方形的个数为:1+3+5=9=32个;图4中小正方形的个数为:1+3+5+7=16=42个;…,
∴第n个图形中有小正方形的个数为:1+3+5+7+…+(2n﹣1)=n2个.
故答案为:(2n﹣1);n2.
(2)∵(2n+1)+(2n+3)+(2n+5)+……+137+139=3300,
∴702﹣n2=3300,
解得:n=40或n=﹣40(舍去).
答:n的值为40.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:
【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:

(1)作出△ABC绕点A逆时针旋转90°的△A1B1C1;作出△ABC关于原点O成中心对称的△A2B2C2;
(2)点B1的坐标为__________,点C2的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
(探究与发现)
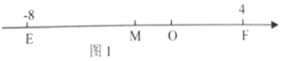
如图1,在数轴上点![]() 表示的数是8,点
表示的数是8,点![]() 表示的数是4,求线段
表示的数是4,求线段![]() 的中点
的中点![]() 所示的数对于求中点表示数的问题,只要用点
所示的数对于求中点表示数的问题,只要用点![]() 所表示的数-8,加上点
所表示的数-8,加上点![]() 所表示的数4,得到的结果再除以2,就可以得到中点
所表示的数4,得到的结果再除以2,就可以得到中点![]() 所表示的数:即
所表示的数:即![]() 点表示的数为:
点表示的数为:![]() .
.
(理解与应用)
把一条数轴在数![]() 处对折,使表示-20和2020两数的点恰好互相重合,则
处对折,使表示-20和2020两数的点恰好互相重合,则![]() .
.
(拓展与延伸)
如图2,已知数轴上有![]() 、
、![]() 、
、![]() 三点,点
三点,点![]() 表示的数是-6,点
表示的数是-6,点![]() 表示的数是8.
表示的数是8.![]() .
.
(1)若点![]() 以每秒3个单位的速度向右运动,点
以每秒3个单位的速度向右运动,点![]() 同时以每秒1个单位的速度向左运动设运动时间为
同时以每秒1个单位的速度向左运动设运动时间为![]() 秒.
秒.
①点![]() 运动
运动![]() 秒后,它在数轴上表示的数表示为 (用含
秒后,它在数轴上表示的数表示为 (用含![]() 的代数式表示)
的代数式表示)
②当点![]() 为线段
为线段![]() 的中点时,求
的中点时,求![]() 的值.
的值.
(2)若(1)中点![]() 、点
、点![]() 的运动速度、运动方向不变,点
的运动速度、运动方向不变,点![]() 从原点以每秒2个单位的速度向右运动,假设
从原点以每秒2个单位的速度向右运动,假设![]() 、
、![]() 、
、![]() 三点同时运动,求多长时间点
三点同时运动,求多长时间点![]() 到点
到点![]() 的距离相等?
的距离相等?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有五张形状、大小、质地都相同的卡片,这些卡片上面分别画有下列图形:①正方形;②等边三角形;③平行四边形;④等腰三角形;⑤圆.将卡片背面朝上洗匀,从中随机抽取一张,抽出的纸片正面图形是轴对称图形,但不是中心对称图形的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
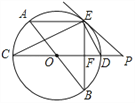
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位:元) | 18 | 12 |
备注 | 1.用不超过16800元购进A,B两类图书共1000本; 2.A类图书不少于600本; …… |
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A,B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲三角形的周长为![]() ,乙三角形的第一条边长为
,乙三角形的第一条边长为![]() ,第二条边长为
,第二条边长为![]() ,第三条边比第二条边短
,第三条边比第二条边短![]() .
.
(1)求乙三角形第三条边的长;
(2)甲三角形和乙三角形的周长哪个大?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十·一”黄金周期间,张家界风景区在7天假期中每天旅游人数变化如下表(正号表示人数比前一天多,负号表示比前天少)
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 单位:万人 | +1.8 | -0.6 | +0.2 | -0.7 | -1.3 | +0.5 | -2.4 |
(1)若9月30日的旅客人数为![]() 万人,则10月4日的旅客人数为_______万人;
万人,则10月4日的旅客人数为_______万人;
(2)七天中旅客人数最多的一天比最少的一天多______万人;
(3)如果每万人带来的经济收入约为120万元,则黄金周七天的旅游总收入约为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
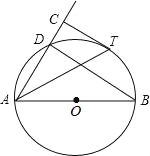
【题目】如图,AB是⊙O的直径,D为⊙O上一点,过![]() 上一点T作⊙O的切线TC,且TC⊥AD于点C.
上一点T作⊙O的切线TC,且TC⊥AD于点C.
(1)若∠DAB=50°,求∠ATC的度数;
(2)若⊙O半径为2,CT=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com