【题目】计算题
（1）
（2）
－
－2
（3）
（代入法） （4）
【答案】（1）-1；（2）
－
；（3）
；（4）
【解析】
先根据二次根式的乘法和除法法则计算，再化简，然后算减法即可；
（2）先根据二次根式的性质化简，再合并同类二次根式即可；
（3）由②得x=13-4y③，把③代入①求出y的值，再把求得的y的值代入③求出x的值即可；
（4）把①×3-②×2求出y的值，再把求得的y的值代入①求出x的值即可.
（1）原式=
=6-7=-1；
（2）原式=
－－
=－；
（3）
，
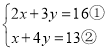由②得
x=13-4y③，
把③代入①得
2(13-4y)+3y=16，
解之得
y=2.
把代入③，得
x=13-4×2=5.
∴；
（4）
，
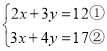①×3-②×2，得
(6x+9y)-(6x+8y)=36-34,
∴y=2，
把y=2代入①，得
2x+6=12,
∴x=3,
∴.
口算题卡加应用题集训系列答案科目：初中数学 来源： 题型：
【题目】如图，平面直角坐标系
中
，
，
．
（1）作出
关于直线
对称的图形△
并写出△各顶点的坐标；
（2）将△向左平移2个单位，作出平移后的△
，并写出△各顶点的坐标；
（3）观察和△，它们是否关于某直线对称？若是，请指出对称轴，并求的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现今“微信运动”被越来越多的人关注和喜爱，某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表（不完整）：
步数 | 频数 | 频率 |
0≤x＜4000 | 8 | a |
4000≤x＜8000 | 15 | 0.3 |
8000≤x＜12000 | 12 | b |
12000≤x＜16000 | c | 0.2 |
16000≤x＜20000 | 3 | 0.06 |
20000≤x＜24000 | d | 0.04 |
请根据以上信息，解答下列问题：
（1）写出a，b，c，d的值并补全频数分布直方图；
（2）本市约有37800名教师，用调查的样本数据估计日行走步数超过12000步（包含12000步）的教师有多少名？
（3）若在50名被调查的教师中，选取日行走步数超过16000步（包含16000步的两名教师与大家分享心得，求被选取的两名教师恰好都在20000步（包含20000步）以上的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
与x轴交于点
，与BC交于点C，连接AC、BC，已知
．
求点B的坐标及抛物线的解析式；
点P是线段BC上的动点
点P不与B、C重合
，连接并延长AP交抛物线于另一点Q，设点Q的横坐标为x．
记
的面积为S，求S关于x的函数表达式并求出当
时x的值；
记点P的运动过程中，
是否存在最大值？若存在，求出的最大值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点B的对应点B′．根据下列条件，利用网格点和三角尺画图：
(1)补全△A′B′C′
(2)画出AC边上的中线BD；
(3)画出AC边上的高线BE；
(4)求△ABD的面积 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一个不透明的袋里装有分别标有数字1，2，3，4，5的5个小球，除所有数字不同外，小球没有其他分别，每次试验前先搅拌均匀．
若从中任取一球，球上的数字为奇数的概率为多少？
若从中任取一球
不放回
，再从中任取1球，请用画树状图或列表的方法求出两个球上的数字之和为偶数的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在
中，
，
，在以AB的中点O为坐标原点，AB所在直线为x轴建立的平面直角坐标系中，将
绕点B时针旋转，使点A旋转至y轴的正半轴上的A处
则图中阴影部分的面积为______
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中(AB＞BC)，AC=2BC，BC边上的中线AD把△ABC的周长分成60和40两部分，则AC=______，AB=________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
