
分析 (1)根据[a]表示不大于a的最大整数,<a>表示大于a的最小整数,进行计算即可;
(2)根据[x]+<x>=2017,可得x+(x+1)=2017,进而得到x=1008;
(3)解方程组可得$\left\{\begin{array}{l}{[x]=-1}\\{<x>=3}\end{array}\right.$,再根据[a]表示不大于a的最大整数,<a>表示大于a的最小整数,即可得到x、y的取值范围.
解答 解:(1)由题可得[-4.5]=-5,<3.01>=4,
故答案为:-5,4;
(2)∵[x]≤x,且x为整数,
∴[x]=x,
∵<x>>x,且x为整数,
∴<x>=x+1,
∵[x]+<x>=2017,
∴x+(x+1)=2017,
解得x=1008;
(3)解原方程组,得$\left\{\begin{array}{l}{[x]=-1}\\{<x>=3}\end{array}\right.$,
又∵[x]表示不大于x的最大整数,<x>表示大于x的最小整数,
∴-1≤x<0,2≤y<3.
点评 本题主要考查了解一元一次不等式组以及二元一次方程组,解题时注意:[a]表示不大于a的最大整数,<a>表示大于a的最小整数.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
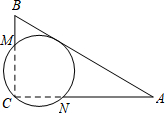 如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,经过点C且与AB边相切的动圆与BC、CA分别相交于点M、N,则线段MN长度的最小值为$\frac{60}{13}$.
如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,经过点C且与AB边相切的动圆与BC、CA分别相交于点M、N,则线段MN长度的最小值为$\frac{60}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
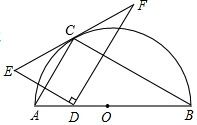 如图,点C在以AB为直径的半圆上,AB=10,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为5$\sqrt{3}$;③当AD=3时,EF与半圆相切;④若点F恰好落在弧BC上,则AD=5;⑤当点D从点A运动到B点时,线段EF扫过的面积是20$\sqrt{3}$.其中正确结论的序号是①②④.
如图,点C在以AB为直径的半圆上,AB=10,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为5$\sqrt{3}$;③当AD=3时,EF与半圆相切;④若点F恰好落在弧BC上,则AD=5;⑤当点D从点A运动到B点时,线段EF扫过的面积是20$\sqrt{3}$.其中正确结论的序号是①②④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com