
【题目】如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
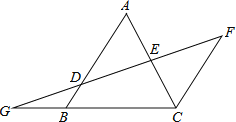
(1)求证:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的长.
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D在一条直线上,BF、CE相交于O,AE=DF,∠E=∠F,OB=OC.

(1)求证:△ACE≌△DBF;
(2)如果把△DBF沿AD折翻折使点F落在点G,连接BE和CG. 求证:四边形BGCE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c(a≠0)的图象上有两点,坐标分别为(x1 , y1),(x2 , y2),其中x1<x2 , y1y2<0,则下列判断正确的是( )
A.a<0
B.a>0
C.方程ax2+bx+c=0必有一根x0满足x1<x0<x2
D.y1<y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则:①∠ABO的度数是 ;
②如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(2)如图3,若AB⊥OM,则是否存在这样的X的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】买一个足球需要m元,买一个篮球需要n元,则买4个足球、7个篮球共需要( )元.
A. 4m+7n B. 28mn C. 7m+4n D. 11mn
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y1=2x+2及直线y2=﹣x+5,.
(1)直线y2=﹣x+5与y轴的交点坐标为 .
(2)在所给的平面直角坐标系(如图)中画出这两条直线的图象;
(3)求这两条直线以及x轴所围成的三角形面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com