
| A. | 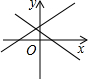 | B. | 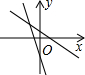 | C. | 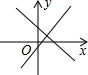 | D. | 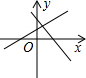 |
分析 对于各选项,先确定一条直线的位置得到a和b的符号,然后根据此符号判断另一条直线的位置是否符号要求.
解答 解:A、若经过第一、二、三象限的直线为y=ax+b,则a>0,b>0,所以直线y=bx+a经过第一、二、三象限,所以A选项错误;
B、若经过第一、二、四象限的直线为y=ax+b,则a<0,b>0,所以直线y=bx+a经过第一、三、四象限,所以B选项错误;
C、若经过第一、三、四象限的直线为y=ax+b,则a>0,b<0,所以直线y=bx+a经过第一、二、四象限,所以C选项正确;
D、若经过第一、二、三象限的直线为y=ax+b,则a>0,b>0,所以直线y=bx+a经过第一、二、三象限,所以D选项错误;
故选C.
点评 本题考查了一次函数图象:一次函数y=kx+b经过两点(0,b)、(-$\frac{b}{k}$,0).注意:使用两点法画一次函数的图象,不一定就选择上面的两点,而要根据具体情况,所选取的点的横、纵坐标尽量取整数,以便于描点准确.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲乙两轮船同时从港口A开出,其中甲轮船每小时航行12海里,乙轮船每小时航行16海里,它们离开港口一个半小时后分别位于B,C两处,且相距30海里,如果甲轮船的航行方向为北偏西40°,请你确定乙轮船的航行方向.
甲乙两轮船同时从港口A开出,其中甲轮船每小时航行12海里,乙轮船每小时航行16海里,它们离开港口一个半小时后分别位于B,C两处,且相距30海里,如果甲轮船的航行方向为北偏西40°,请你确定乙轮船的航行方向.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了了解奥运知识,某中学举行了一次“奥运知识竞赛”,共有900名学生参加了这次竞赛,为了了解本次竞赛情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分),进行统计,请你根据下面尚未完成的统计表和统计图,解答下列问题.
为了了解奥运知识,某中学举行了一次“奥运知识竞赛”,共有900名学生参加了这次竞赛,为了了解本次竞赛情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分),进行统计,请你根据下面尚未完成的统计表和统计图,解答下列问题.| 分组 | 频数 | 频率 |
| 50.5~60.5 | 3 | 0.06 |
| 60.5~70.5 | 9 | A |
| 70.5~80.5 | 11 | 0.22 |
| 80.5~90.5 | 15 | 0.30 |
| 90.5~100.5 | B | C |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°,(sin39°≈0.63,cos39°≈0.78,tan39°≈0.81)
目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°,(sin39°≈0.63,cos39°≈0.78,tan39°≈0.81)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,E,F分别是正方形ABCD的边BC,CD上的点,且BE=CF,连接AE,BF,将△ABE绕正方形的中心按逆时针方向旋转α(0<α<180°)到∠BCF,则旋转角α等于( )
如图,E,F分别是正方形ABCD的边BC,CD上的点,且BE=CF,连接AE,BF,将△ABE绕正方形的中心按逆时针方向旋转α(0<α<180°)到∠BCF,则旋转角α等于( )| A. | 90° | B. | 60° | C. | 45° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com