
【题目】如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
(1)求该抛物线所对应的函数关系式;
(2)设抛物线上的一个动点P的横坐标为t(0<t<3),过点P作PD⊥BC于点D. ① 求线段PD的长的最大值;② 当BD=2CD时,求t的值;
(3)若点Q是抛物线的对称轴上的动点,抛物线上存在点M,使得以B、C、Q、M为顶点的四边形为平行四边形,请求出所有满足条件的点M的坐标.

【答案】(1) y=-x2+2x+3;(2)①![]() ;②2;(3) (2,3)或(4,-5)或(-2,-5).
;②2;(3) (2,3)或(4,-5)或(-2,-5).
【解析】试题分析: (1)将A、B、C三点的坐标代入y=a(x+1)(x-3)即可求出抛物线的解析式.
(2)①过点P作PE⊥x轴于点E,交BC于点F,求出△PBC的最大面积,即可求出PD的最大值.
②过点D作DG⊥x轴于点G,由于DG∥OC,从而可知![]() ,从而可求出t的值.
,从而可求出t的值.
(3)由于BC是B、C、Q、M为顶点的四边形中的一条固定的线段,因此将此线段分为平行四边形的边和对角线进行讨论即可求出M的坐标.
试题解析:
(1)设抛物线所对应的函数关系式为![]()
将A(-1,0),B(3,0),C(0,3)代入![]() 得:
得:
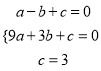
解得: 
∴抛物线所对应的函数关系式为![]()
(2)①设点P的坐标为(t, ![]() )
)
过P作PN⊥x轴于点F,交BC于点E
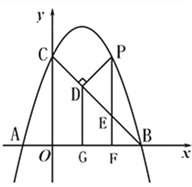
设直线BC解析式为y=kx+b
把B(3,0),C(0,3)代入y=kx+b得
![]() 解得:k=-1,b=3
解得:k=-1,b=3
∴直线BC解析式为y=-x+3
∴点E坐标为(t, ![]() )
)
PE=![]() -(
-(![]() )=
)=![]()
∵OB=OC=3,∴∠OBC=45°
∵PD⊥BC
∴∠PED=45°
∴PD=PE×sin45°=![]() PE=
PE=![]() (
(![]() )=-
)=-![]()
![]()
![]()
∴当t=![]() 时,PD的最大面积为
时,PD的最大面积为![]()
②过D作DG⊥x轴于点G,则DG∥OC
∴△BOC∽△BGD
∴![]()
当BD=2CD时,BD:BC=2:3
![]()
∴DG=2,即点D的纵坐标为2
把y=2代入y=-x+3得x=1
∴D点坐标为(1,2)
设直线PD解析式为:y=x+b
把D(1,2)代入上式得:
2=1+b,
解得:b=1
∴直线PD解析式为y=x+1
解方程组![]() 得:
得: ![]() ,
, ![]() ( 舍去)
( 舍去)
∴当BD=2CD时,t的值为2
{或∵△PDE是等腰直角三角形,∴![]() )
)
即![]() ,
,
解得: ![]() ,
, ![]() ( 舍去)}
( 舍去)}
(3)∵点Q是抛物线![]() 的对称轴x=1上的动点,
的对称轴x=1上的动点,
∴点Q的横坐标为1,
∵点M在抛物线![]() 上,∴设点M的坐标为(m,
上,∴设点M的坐标为(m, ![]() )
)
(I)如图,当BC、QM为平行四边形的对角线时,
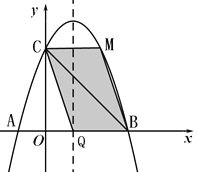
可得: ![]()
即:3=1+m,
∴m=2
∴点M坐标为(2,3)
(II)如图,当BQ、MC为平行四边形的对角线时,
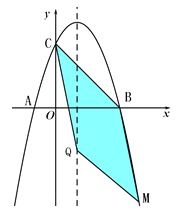
可得: ![]()
即:3+1=m,
∴m=4
∴点M坐标为(4,-5)
(III)如图,当BM、QC为平行四边形的对角线时,

可得: ![]()
即:3+m=1,
∴m=-2
∴点M坐标为(-2,-5)
综合以上所述,满足平行四边形的点M的坐标为(2,3)或(4,-5)或(-2,-5)
点睛: 本题难度较大,考查的是二次函数图象与解析式的灵活运用,一般这样题目都是作为压轴题出现,考生平时应多积累二次函数的综合知识.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】下列是随机事件的是( )
A. 口袋里共有5个球,都是红球,从口袋里摸出1个球是黄球
B. 平行于同一条直线的两条直线平行
C. 掷一枚图钉,落地后图钉针尖朝上
D. 掷一枚质地均匀的骰子,掷出的点数是7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,是不确定事件的是( )
A. 三条线段可以组成一个三角形B. 内错角相等,两条直线平行
C. 对顶角相等D. 平行于同一条直线的两条直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,牛牛去图书城买书,导购员阿姨对牛牛说:“你在这里花10元钱办一张会员卡,买书可以享受9折优惠哦。”牛牛在心里算了一算发现,如果办一张会员卡,再把自己想要的书全买了还可以节省8元钱,于是很快就去办了一张会员卡。请问:你知道牛牛所买的书籍原价一共要多少钱吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
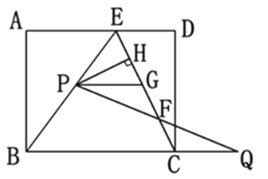
【题目】如图,在矩形ABCD中,E是AD上一点,AB=8,BE=BC=10,动点P在线段BE上(与点B、E不重合),点Q在BC的延长线上,PE=CQ,PQ交EC于点F,PG∥BQ交EC于点G,设PE=x.
(1)求证:△PFG≌△QFC
(2)连结DG.当x为何值时,四边形PGDE是菱形,请说明理由;
(3)作PH⊥EC于点H.探究:
①点P在运动过程中,线段HF的长度是否发生变化?若变化,说明理由;若不变,求HF的长度;
②当x为何值时,△PHF与△BAE相似
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com