
【题目】如图,在平面直角坐标系xOy中,△ABC的边AC在x轴上,边BC⊥x轴,双曲线y= ![]() 与边BC交于点D(4,m),与边AB交于点E(2,n).
与边BC交于点D(4,m),与边AB交于点E(2,n).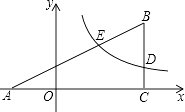
(1)求n关于m的函数关系式;
(2)若BD=2,tan∠BAC= ![]() ,求k的值和点B的坐标.
,求k的值和点B的坐标.
【答案】
(1)
解:∵点D(4,m),点E(2,n)在双曲线y= ![]() 上,
上,
∴4m=2n,解得n=2m;
(2)
解:过点E作EF⊥BC于点F,

∵由(1)可知n=2m,
∴DF=m,
∵BD=2,
∴BF=2﹣m,
∵点D(4,m),点E(2,n),
∴EF=4﹣2=2,
∵EF∥x轴,
∴tan∠BAC=tan∠BEF= ![]() =
= ![]() =
= ![]() ,解得m=1,
,解得m=1,
∴D(4,1),
∴k=4×1=4,B(4,3).
【解析】(1)直接根据反比例函数中k=xy的特点进行解答即可;(2)过点E作EF⊥BC于点F,根据(1)中m、n的关系可得出DF=m,故BF=2﹣m,再由点D(4,m),点E(2,n)可知EF=4﹣2=2,再根据EF∥x轴可知tan∠BAC=tan∠BEF= ![]() ,由此即可得出结论.
,由此即可得出结论.
【考点精析】解答此题的关键在于理解反比例函数的图象的相关知识,掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点,以及对反比例函数的性质的理解,了解性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】阅读并填空:
寻求某些勾股数的规律:
⑴对于任何一组已知的勾股数都扩大相同的正整数倍后,就得到了一组新的勾股数.例如:![]() ,我们把它扩大2倍、3倍,就分别得到
,我们把它扩大2倍、3倍,就分别得到![]() 和
和![]() ,……若把它扩大11倍,就得到 ,若把它扩大n倍,就得到 .
,……若把它扩大11倍,就得到 ,若把它扩大n倍,就得到 .
⑵对于任意一个大于1的奇数,存在着下列勾股数:
若勾股数为3,4,5,因为,则有![]() ;
;
若勾股数为5,12,13,则有![]() ;
;
若勾股数为7,24,25,则有 ;……
若勾股数为m(m为奇数),n, ,则有m2= ,用m来表示n= ;
当m=17时,则n= ,此时勾股数为 .
⑶对于大于4的偶数:
若勾股数为6,8,10,因为![]() ,则有……请找出这些勾股数之间的关系,并用适当的字母表示出它的规律来,并求当偶数为24的勾股数.
,则有……请找出这些勾股数之间的关系,并用适当的字母表示出它的规律来,并求当偶数为24的勾股数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“美丽广西,清洁乡村”活动中,李家村村长提出了两种购买垃圾桶方案;方案1:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用250元;方案2:买不分类垃圾桶,需要费用1000元,以后每月的垃圾处理费用500元;设方案1的购买费和每月垃圾处理费共为y1元,交费时间为x个月;方案2的购买费和每月垃圾处理费共为y2元,交费时间为x个月.
(1)直接写出y1、y2与x的函数关系式;
(2)在同一坐标系内,画出函数y1、y2的图象;
(3)在垃圾桶使用寿命相同的情况下,哪种方案省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD.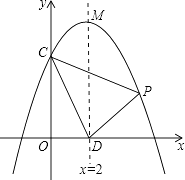
(1)求该抛物线的解析式;
(2)设点P(x,y)是第一象限内该抛物线上的一个动点,△PCD的面积为S,求S关于x的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,若经过点P的直线PE与y轴交于点E,是否存在以O、P、E为顶点的三角形与△OPD全等?若存在,请求出直线PE的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2平移后的位置如图所示,点A,B坐标分别为(﹣1,0)、(3,0),设平移后的抛物线与y轴交于点C,其顶点为D.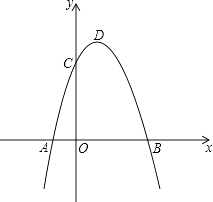
(1)求平移后的抛物线的解析式和点D的坐标;
(2)∠ACB和∠ABD是否相等?请证明你的结论;
(3)点P在平移后的抛物线的对称轴上,且△CDP与△ABC相似,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
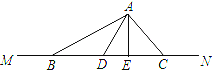
【题目】如图,MN是一条东西朝向的笔直的公路,C是位于该公路上的一个检测点辆长为9m的小货车BD行驶在该公路上小王位于点A处观察小货车,某时刻他发现车头D、车尾B及检测点C分别距离他10m、17m,2![]() m
m
(1)过点A向MN引垂线,垂足为E,请利用勾股定理分别找出线段AE与DE、AE与BE之间所满足的数量关系;
(2)在上一问的提示下,继续完成下列问题:
①求线段DE的长度;
②该小货车的车头D距离检测点C还有多少m?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图可以近似地刻画下列哪个情景( )
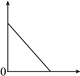
A. 小明匀速步行上学时离学校的距离与时间的关系
B. 匀速行驶的汽车的速度与时间的关系
C. 小亮妈妈到超市购买苹果的总费用与苹果质量的关系
D. 一个匀速上升的气球的高度与时间的关系
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com