
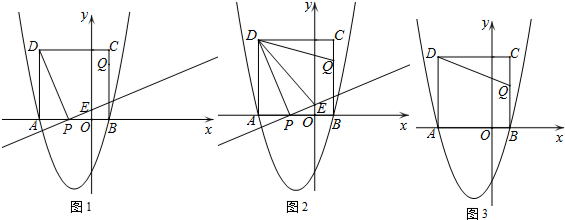
分析 (1)先将点B的坐标代入解析式求得c的值确定二次函数解析式,令y=0即可求得A点坐标;
(2)由DP⊥PE证得△DAP∽△POE,用比例式表示出y与t的关系,根据函数图象的性质可求得OE的最大值;
(3)需要分类讨论:根据t的不同取值得出相似三角形,再由相似的性质可得t的取值;
(4)先证明△DCQ≌△DC′Q,从而得到∠CDQ=∠C′DQ,DC′=DC=4,再得出∠CDQ=30°,即可求得满足条件的t值.
解答 解:(1)把B(1,0)代入y=x2+2x+c得c=-3.
∴y=x2+2x-3.
由x2+2x-3=0得x1=-3,x2=1.
∴点A的坐标为(-3,0).
(2)如图(2),由正方形ABCD得AD=AB=4.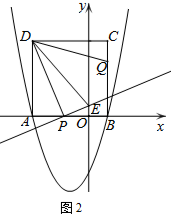
由DP⊥PE证得△DAP∽△POE,
∴$\frac{AD}{OP}=\frac{AP}{OE}$ 设OE=y,则$\frac{4}{3-2t}=\frac{2t}{y}$.
∴$y=\frac{1}{2}(3-2t)•t=-(t-\frac{3}{4})^{2}+\frac{9}{16}$.
∵a=-1<0
∴当t=$\frac{3}{4}$(属于0<t<$\frac{3}{2}$)时,${y}_{最大}=\frac{9}{16}$,此时$2t=\frac{3}{2}$,
即点P位于AO的中点时,
线段OE的长有最大值$\frac{9}{16}$.
(3)①如图①,当0<t<$\frac{3}{2}$时,△DPE∽△DCQ,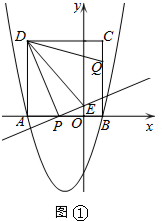
∴$\frac{DP}{PE}=\frac{DC}{CQ}$.又△ADP∽△OPE,
∴$\frac{DP}{PE}=\frac{AD}{OP}$.
∴$\frac{AD}{OP}=\frac{DC}{CQ}$.即$\frac{4}{3-2t}=\frac{4}{t}$,解得t=1.
经检验:t=1是原方程的解.
②如图②,当$\frac{3}{2}<t≤\frac{7}{2}$时,同理证得△ADP∽△OPE,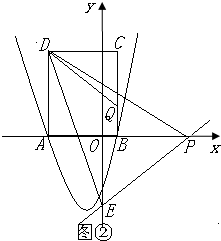
∴$\frac{AD}{OP}=\frac{DC}{CQ}$.
即$\frac{4}{2t-3}=\frac{4}{t}$,解得t=3.经检验:t=3是原方程的解.
③如图③,当$\frac{7}{2}<t≤4$时,△DPE∽△QCD,
∴$\frac{DP}{PE}=\frac{QC}{CD}$.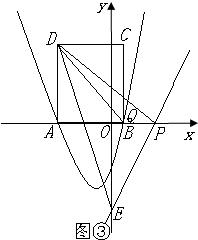
同理得$\frac{DP}{PE}=\frac{AD}{OP}$.
∴$\frac{AD}{OP}=\frac{QC}{CD}$.即$\frac{4}{2t-3}=\frac{t}{4}$,解得${t}_{1}=\frac{3+\sqrt{137}}{4},{t}_{2}=\frac{3-\sqrt{137}}{4}$(经检验:舍去${t}_{2}=\frac{3-\sqrt{137}}{4}$).
综上所述,t=1或3或$\frac{3+\sqrt{137}}{4}$.
(4)存在$t=\frac{4\sqrt{3}}{3}$.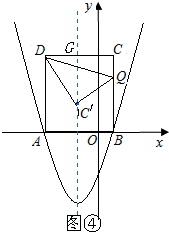
理由如下:如图
由△DCQ沿DQ翻折得△DC′Q,则△DCQ≌△DC′Q,
∴∠CDQ=∠C′DQ,DC′=DC=4.
设抛物线的对称轴交DC于G,则DG=2.在Rt△DC′G中,
∵C′D=2DG,
∴∠C′DG=60°.
∴$∠CDQ=\frac{1}{2}×60°=30°$.
∴CQ=$\frac{4\sqrt{3}}{3}$,即t=$\frac{4\sqrt{3}}{3}$.
点评 本题是二次函数的综合题型,其中涉及到运用待定系数法求二次函数的解析式,相似三角形的性质与一判定,二次函数的最值等知识,综合性较强,难度适中.运用数形结合、分类讨论及方程思想是解题的关键.


科目:初中数学 来源: 题型:解答题
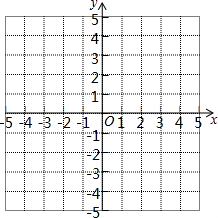 在如图的直角坐标系中,画出点A(-1,-1),B(3,-1),C(4,2),D(0,2),并将各点依次用线段连接起来,求图形ABCD的面积.(每个小方格的长和宽都为一个长度单位)
在如图的直角坐标系中,画出点A(-1,-1),B(3,-1),C(4,2),D(0,2),并将各点依次用线段连接起来,求图形ABCD的面积.(每个小方格的长和宽都为一个长度单位)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
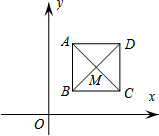 如图,已知正方形ABCD,顶点A(1,3),B(1,1),C(3,1),对角线交于点M.规定“把正方形ABCD先沿x轴翻折,再向左平移个单位”为一次变换,那么经过两次变换后,点M的坐标变为(0,2),连续经过2015次变换后,点M的坐标变为(-2013,-2).
如图,已知正方形ABCD,顶点A(1,3),B(1,1),C(3,1),对角线交于点M.规定“把正方形ABCD先沿x轴翻折,再向左平移个单位”为一次变换,那么经过两次变换后,点M的坐标变为(0,2),连续经过2015次变换后,点M的坐标变为(-2013,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
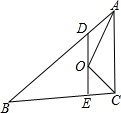 如图,在△ABC中,AB=5cm,BC=3cm,∠BAC与∠BCA的平分线相交于点O,点D在AB上,且AD=OD.DO的延长线交BC于E.试求△BDE的周长.
如图,在△ABC中,AB=5cm,BC=3cm,∠BAC与∠BCA的平分线相交于点O,点D在AB上,且AD=OD.DO的延长线交BC于E.试求△BDE的周长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com