
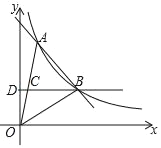
����Ŀ����ͼ��һ�κ���y��kx+b��k��0���뷴��������y��![]() ��a��0����ͼ���ڵ�һ������A��B���㣬A�������Ϊ��m��4����B�������Ϊ��3��2��������OA��OB����B��BD��y�ᣬ����ΪD����OA��C����OC��CA��
��a��0����ͼ���ڵ�һ������A��B���㣬A�������Ϊ��m��4����B�������Ϊ��3��2��������OA��OB����B��BD��y�ᣬ����ΪD����OA��C����OC��CA��
��1����һ�κ����ͷ����������ı���ʽ��
��2�����AOB�������
��3����ֱ��BD���Ƿ����һ��E��ʹ�á�AOE��ֱ�������Σ�������п��ܵ�E�����꣮
���𰸡���1��y��![]() ��y����
��y����![]() x+6����2��
x+6����2��![]() ����3��E��������
����3��E��������![]() ��2����
��2����![]() ��2����
��2����![]() ��2����
��2����![]() ��2����
��2����
��������
��1�������ô���ϵ���������������������ʽ������ȷ������A�����꣬���ô���ϵ�������һ�κ�������ʽ��
��2������A��AF��x����F��OB��G�������OB�Ľ���ʽ���������AG���������ε������ʽ���ɵó����ۣ�
��3�����������ηֱ�������⼴�ɽ�����⣻
�⣺��1���ߵ�B��3��2���ڷ���������y��![]() ��ͼ���ϣ�
��ͼ���ϣ�
��a��3��2��6��
�෴���������ı���ʽΪy��![]() ��
��
�ߵ�A��������Ϊ4��
�ߵ�A�ڷ���������y��![]() ͼ���ϣ�
ͼ���ϣ�
��A��![]() ��4����
��4����
�� ����
����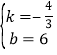 ��
��
��һ�κ����ı���ʽΪy����![]() x+6��
x+6��
��2����ͼ1������A��AF��x����F��OB��G��

��B��3��2����
��ֱ��OB�Ľ���ʽΪy��![]() x��
x��
��G��![]() ��1����
��1����
A��![]() ��4����
��4����
��AG��4��1��3��
��S��AOB��S��AOG+S��ABG��![]() ��3��3��
��3��3��![]() ��
��
��3����ͼ2�У�
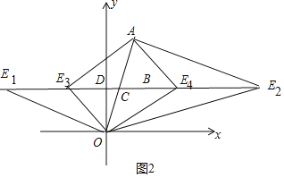
����AOE1��90��ʱ����ֱ��AC�Ľ���ʽΪy��![]() x��
x��
��ֱ��OE1�Ľ���ʽΪy����![]() x��
x��
��y��2ʱ��x����![]() ��
��
��E1����![]() ��2����
��2����
����OAE2��90��ʱ��
ֱ��OE1ƽ��ֱ��OE2
��ֱ��OE2�Ľ���ʽΪy����![]() x+b��
x+b��
��ֱ�߹���A��![]() ��4������b=
��4������b=![]()
��ֱ��OE2�Ľ���ʽΪy����![]() x+
x+![]() ��
��
��y��2ʱ��x��![]() ��
��
��E2��![]() ��2����
��2����
����OEA��90��ʱ��
��A��![]() ��4������OA=
��4������OA=![]()
��AC��OC��CE��![]() ��
��
��C��![]() ��2����
��2����
��ɵ�E3��![]() ��2����E4��
��2����E4��![]() ��2����
��2����
�������������������ĵ�E����Ϊ����![]() ��2����
��2����![]() ��2����
��2����![]() ��2����
��2����![]() ��2����
��2����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���������![]() ����A�ĺ�������
����A�ĺ�������![]() ������y�ύ�ڵ�
������y�ύ�ڵ�![]() ����PΪ��������һ�㣮
����PΪ��������һ�㣮
![]() �������ߵı���ʽ��
�������ߵı���ʽ��
![]() ����������
����������![]() ����ƽ��4����λ����Pƽ�ƺ�Ķ�Ӧ��Ϊ
����ƽ��4����λ����Pƽ�ƺ�Ķ�Ӧ��Ϊ![]() ���
���![]() �����Q�����꣮
�����Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��ƽ����
��ƽ����![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊֱ������
Ϊֱ������![]() .
.

(1)��֤��![]() �ǡ�
�ǡ�![]() �����ߣ�
�����ߣ�
(2) ��AC=3��BC=4����BE�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ԫ���ڼ䣬ij�̳��ƻ������ס���������Ʒ��
��1����֪�ס���������Ʒ�Ľ��۷ֱ�Ϊ30Ԫ��70Ԫ�����̳������ס���������Ʒ��50����Ҫ2300Ԫ������̳������ס���������Ʒ�����ټ���
��2�����̳���Ͷ��9500Ԫ�ʽ���������Ʒ���ɼ�����������Ʒ�Ľ������ۼ������ʾ��
�� | �� | |
���ۣ�Ԫ/���� | 30 | 70 |
�ۼۣ�Ԫ/���� | 50 | 100 |
��ȫ���������ɻ���5000Ԫ�������ۼ۩����ۣ���������������̳������ס���������Ʒ�����ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
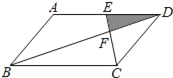
����Ŀ����ͼ��ƽ���ı���ABCD�У�EΪAD���е㣬��֪��DEF�����Ϊ1����ƽ���ı���ABCD�����Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ʵʩ��ҵ����ƶ������ƶ�����а���ɽ��ֲijƷ�����֣���֪�����ֵijɱ���Ϊ6Ԫ/ǧ�ˣ������ջ�Ͷ���г�����ʱ�������г�������ָ����ֲ����������ÿ���������y��ǧ�ˣ������۵���x��Ԫ��֮��ĺ�����ϵ��ͼ��ʾ��
��1����y��x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2������Ʒ�����ֶ���Ϊ����ʱ��ÿ�����ۻ�õ����������������Ƕ��٣�
��3��ij��ũ�����깲��ժ����12000ǧ�ˣ�����Ʒ�����ֵı�����Ϊ50�죬���գ�2�������۷�ʽ���ܷ��ڱ�������ȫ���������������֣����ܣ���˵�����ɣ������ܣ�Ӧ�����ۼ�Ϊ����Ԫʱ���������������ܻ���������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
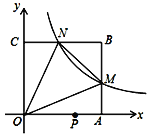
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����������![]() ��ͼ����߳���6��������
��ͼ����߳���6��������![]() ������
������![]() �ֱ��ཻ��
�ֱ��ཻ��![]() ���㣬
���㣬![]() �����Ϊ10.������
�����Ϊ10.������![]() ��
��![]() ���ϣ���
���ϣ���![]() ����Сֵ��_____________
����Сֵ��_____________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
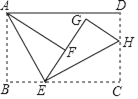
����Ŀ����ͼ������ABCD�У�AB��4��AD��6����EΪBC��һ�㣬����ABE��AE�۵��õ���AEF����HΪCD��һ�㣬����CEH��EH�۵��õ���EHG����F�����߶�EG�ϣ���GF��GHʱ����BE�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
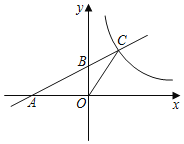
����Ŀ����ͼ��ֱ��l��x�ᣬy��ֱ���A��B���㣬���뷴��������y��![]() ��x��0����ͼ���ڵ�C����S��AOB��S��BOC��1����k����������
��x��0����ͼ���ڵ�C����S��AOB��S��BOC��1����k����������
A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com