
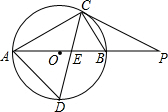
 如图,⊙O是△ABC的外接圆,AB是直径,∠CAB=30°,BC=1,∠ACB的平分线交⊙O于点D,交AB于点E.
如图,⊙O是△ABC的外接圆,AB是直径,∠CAB=30°,BC=1,∠ACB的平分线交⊙O于点D,交AB于点E.分析 (1)连接BD,在Rt△ABC中,可求得AB、AC,又可知△ABD为等腰直角三角形,可求得AD;
(2)连接OC,可先证明△OBC为等边三角形,当PC为切线时,可求得BP=BC,可得出结论.
解答 解:
(1)如图1,连接BD,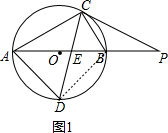
∵AB是直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,
∵∠CAB=30°,BC=1,
∴AB=2,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∵CD平分∠ACB,
∴△ABD为等腰直角三角形,
∴AD=BD=$\frac{\sqrt{2}}{2}$AB=$\sqrt{2}$;
(2)如图2,连接OC,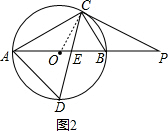
∵∠CAB=30°,
∴∠COB=60°,
∴△OBC为等边三角形,
当PC为⊙O的切线时,则∠OCP=90°,
∴∠BCP=∠BPC=30°,
∴PB=BC=1,
即当PB=1时,PC与⊙O相切.
点评 本题主要考查切线判定和性质及解直角三角形,掌握切线的判定方法是解题的关键,即有切点时连接圆心和切点,然后证明垂直,没有切点时,过圆心作垂直,证明圆心到直线的距离等于半径.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:选择题
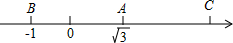 如图,数轴上A、B两点对应的实数是$\sqrt{3}$和-1,AC=AB,则点C所对应的实数是( )
如图,数轴上A、B两点对应的实数是$\sqrt{3}$和-1,AC=AB,则点C所对应的实数是( )| A. | 1+$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 2$\sqrt{3}$-1 | D. | 2$\sqrt{3}$+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
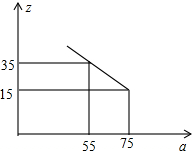 某工厂投入生产一种机器,当该机器生产数量至少10台,但不超过70台,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如表:
某工厂投入生产一种机器,当该机器生产数量至少10台,但不超过70台,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如表:| x(单位:台) | 10 | 20 | 30 |
| y(单位:万元∕台) | 60 | 55 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | Rt△ABD中斜边BD上的高为6 | |
| B. | 无论点P在AD上何处,PM与PN的和始终保持不变 | |
| C. | 当x=3时,OP垂直平分AD | |
| D. | 若AD=10,则矩形ABCD的面积为60 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
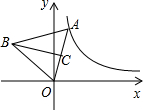 如图,在平面直角坐标系中,点A是双曲线y=$\frac{4}{x}$(x>0)上一动点,以OA为边作等边△AOB,高BC的最小值为$\sqrt{6}$.
如图,在平面直角坐标系中,点A是双曲线y=$\frac{4}{x}$(x>0)上一动点,以OA为边作等边△AOB,高BC的最小值为$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com