练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    抛物线y＝ax2的对称轴是________．

    答案：y轴
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖北省随州市2010年初中毕业生升学考试数学试题 题型：059

    已知抛物线y＝ax2＋bx＋c(a≠0)顶点为C(1，1)且过原点O．过抛物线上一点P(x，y)向直线y＝作垂线，垂足为M，连FM(如图)．

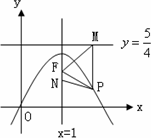
    (1)求字母a，b，c的值；

    (2)在直线x＝1上有一点F(1，)，求以PM为底边的等腰三角形PFM的P点的坐标，并证明此时△PFM为正三角形；

    (3)对抛物线上任意一点P，是否总存在一点N(1，t)，使PM＝PN恒成立，若存在请求出t值，若不存在请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

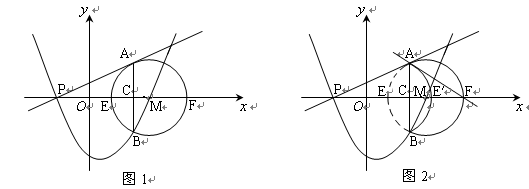
    如图1，在平面直角坐标系中，已知点M的坐标是（3，0），半径为2的⊙M交x轴于E、F

    两点，过点P（－1，0）作⊙M的切线，切点为点A，过点A作AB⊥x轴于点C，交⊙M于

    点B。抛物线y＝ax2＋bx＋c经过P、B、M三点。

    1.（1）求该抛物线的函数表达式；（3分）

    2.（2）若点Q是抛物线上一动点，且位于P、B两点之间，设四边形APQB的面积为S，点Q的

    横坐标为x，求S与x之间的函数关系式，并求S的最大值和此时点Q的坐标；（4分）

    3.（3）如图2，将弧AEB沿弦AB对折后得到弧AE′B，试判断直线AF与弧AE′B的位置关系，

    并说明理由。（3分）

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，在平面直角坐标系中，已知点M的坐标是（3，0），半径为2的⊙M交x轴于E、F
    两点，过点P（－1，0）作⊙M的切线，切点为点A，过点A作AB⊥x轴于点C，交⊙M于
    点B。抛物线y＝ax2＋bx＋c经过P、B、M三点。

    【小题1】（1）求该抛物线的函数表达式；（3分）
    【小题2】（2）若点Q是抛物线上一动点，且位于P、B两点之间，设四边形APQB的面积为S，点Q的
    横坐标为x，求S与x之间的函数关系式，并求S的最大值和此时点Q的坐标；（4分）
    【小题3】（3）如图2，将弧AEB沿弦AB对折后得到弧AE′B，试判断直线AF与弧AE′B的位置关系，
    并说明理由。（3分）

    查看答案和解析>>

    科目：初中数学 来源：2011年广东省深圳市宝安区中考模拟数学卷 题型：解答题

    如图1，在平面直角坐标系中，已知点M的坐标是（3，0），半径为2的⊙M交x轴于E、F
    两点，过点P（－1，0）作⊙M的切线，切点为点A，过点A作AB⊥x轴于点C，交⊙M于
    点B。抛物线y＝ax2＋bx＋c经过P、B、M三点。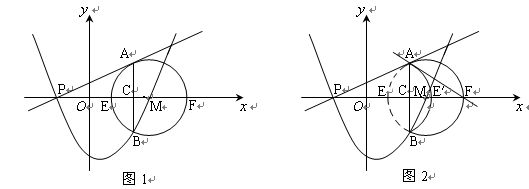

    【小题1】（1）求该抛物线的函数表达式；（3分）
    【小题2】（2）若点Q是抛物线上一动点，且位于P、B两点之间，设四边形APQB的面积为S，点Q的
    横坐标为x，求S与x之间的函数关系式，并求S的最大值和此时点Q的坐标；（4分）
    【小题3】（3）如图2，将弧AEB沿弦AB对折后得到弧AE′B，试判断直线AF与弧AE′B的位置关系，
    并说明理由。（3分）

    查看答案和解析>>

    科目：初中数学 来源：2011年广东省深圳市宝安区中考模拟数学卷 题型：解答题

    如图1，在平面直角坐标系中，已知点M的坐标是（3，0），半径为2的⊙M交x轴于E、F

    两点，过点P（－1，0）作⊙M的切线，切点为点A，过点A作AB⊥x轴于点C，交⊙M于

    点B。抛物线y＝ax2＋bx＋c经过P、B、M三点。

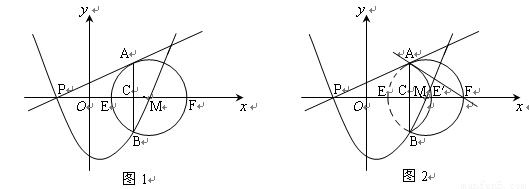
    1.（1）求该抛物线的函数表达式；（3分）

    2.（2）若点Q是抛物线上一动点，且位于P、B两点之间，设四边形APQB的面积为S，点Q的

    横坐标为x，求S与x之间的函数关系式，并求S的最大值和此时点Q的坐标；（4分）

    3.（3）如图2，将弧AEB沿弦AB对折后得到弧AE′B，试判断直线AF与弧AE′B的位置关系，

    并说明理由。（3分）

     

    查看答案和解析>>

    同步练习册答案