
【题目】如图,AB∥CD,AB=CD,点B、E、F、D在同一条直线上,∠BAE=∠DCF.
(1)求证:AE=CF;
(2)连结AF、EC,试猜想四边形AECF是什么四边形,并证明你的结论.
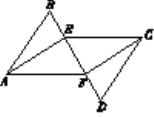
【答案】(1)证明见解析(2)四边形AECF是平行四边形
【解析】
(1)要证AE=CF,可证△ABE≌△CDF.由AB∥CD,可知∠B=∠D,由AB=CD,已知∠BAE=∠DCF,即可证得.
(2)由△ABE≌△CDF得AE=CF,∠AEB=∠CFD,故180°-∠AEB=180°-∠CFD,即∠AEF=∠CFE,AE∥CF,AE=CF,故四边形AECF是平行四边形.
(1)证明:∵AB∥CD,∴∠B=∠D.
在△ABE和△CDF中,
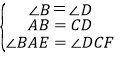 ,
,
∴△ABE≌△CDF,
∴AE=CF.
(2)四边形AECF是平行四边形.
证明:由(1)△ABE≌△CDF得AE=CF,∠AEB=∠CFD,
∴180°-∠AEB=180°-∠CFD,
即∠AEF=∠CFE.
∴AE∥CF.
又∵AE=CF,
∴四边形AECF是平行四边形.
故答案为:(1)证明见解析(2)四边形AECF是平行四边形.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】课堂上学习了勾股定理后,知道“勾三、股四、弦五”.王老师给出一组数让学生观察:3、4、5;5、12、13;7、24、25;9、40、41;…,学生发现这些勾股 数的勾都是奇数,且从 3 起就没有间断过,于是王老师提出以下问题让学生解决.
(1)请你根据上述的规律写出下一组勾股数:11、________、________;
(2)若第一个数用字母a(a为奇数,且a≥3)表示,那么后两个数用含a的代数式分别怎么表示?小明发现每组第二个数有这样的规律4=![]() ,12=
,12=![]() ,24=
,24=![]() ……,于是他很快表示了第二数为
……,于是他很快表示了第二数为 ![]() ,则用含a的代数式表示第三个数为________;
,则用含a的代数式表示第三个数为________;
(3)用所学知识证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们来定义下面两种数:
(一)平方和数:若一个三位数或者三位以上的整数分拆成最左边、中间、最右边三个数后满足:中间数=(最左边数)2+(最右边数)2,我们就称该整数为平方和数.
例如:对于整数251.它中间的数字是5,最左边数是2,最右边数是1.
![]() 是一个平方和数
是一个平方和数
又例如:对于整数3254,它的中间数是25,最左边数是3,最右边数是4,
![]() 是一个平方和数.当然152和4253这两个数也是平方和数;
是一个平方和数.当然152和4253这两个数也是平方和数;
(二)双倍积数:若一个三位数或者三位以上的整数分拆成最左边、中间、最右边三个数后满足:中间数=![]() 最左边数
最左边数![]() 最右边数,我们就称该整数为双倍积数.
最右边数,我们就称该整数为双倍积数.
例如:对于整数163,它的中间数是6,最左边数是1,最右边数是3,
![]() 是一个双倍积数,
是一个双倍积数,
又例如:对于整数3305,它的中间数是30,最左边数是3,最右边数是5,
![]() 是一个双倍积数,当然361和5303这两个数也是双倍积数.
是一个双倍积数,当然361和5303这两个数也是双倍积数.
注意:在下面的问题中,我们统一用字母![]() 表示一个整数分拆出来的最左边数,用字母
表示一个整数分拆出来的最左边数,用字母![]() 表示该整数分拆出来的最右边数,请根据上述定义完成下面问题:
表示该整数分拆出来的最右边数,请根据上述定义完成下面问题:
(1)①若一个三位整数为平方和数,且十位数为4,则该三位数为________;
②若一个三位整数为双倍积数,且十位数字为 6 ,则该三位数为_________;
③若一个整数既为平方和数,又是双倍积数,则![]() 应满足的数量关系为_______;
应满足的数量关系为_______;
(2)若![]() (即这是个最左边数为
(即这是个最左边数为![]() ,中间数为565,最右边数为
,中间数为565,最右边数为![]() 的整数,以下类同)是一个平方和数,
的整数,以下类同)是一个平方和数,![]() 是一个双倍积数,求
是一个双倍积数,求![]() 的值.
的值.
(3)从所有三位整数中任选一个数为双倍积数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为反比例函数y= ![]() (k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A、B.若∠AOB=135°,则k的值是( )
(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A、B.若∠AOB=135°,则k的值是( )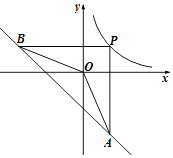
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自由转动如图所示的转盘.下列事件中哪些是必然事件?那些是随机事件?根据你的经验,将这些事件的序号按发生的可能性从小到大的顺序排列.

(1)转盘停止后指针指向1;
(2)转盘停止后指针指向10;
(3)转盘停止后指针指向的是偶数;
(4)转盘停止后指针指向的不是奇数就是偶数;
(5)转盘停止后指针指向的数大于1.
查看答案和解析>>
科目:初中数学 来源: 题型:
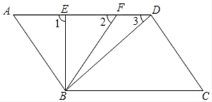
【题目】如图,已知AD∥BC,∠A=∠C=50°,线段AD上从左到右依次有两点E、F(不与A、D重合)
(1)AB与CD是什么位置关系,并说明理由;
(2)观察比较∠1、∠2、∠3的大小,并说明你的结论的正确性;
(3)若∠FBD:∠CBD=1:4,BE平分∠ABF,且∠1=∠BDC,求∠FBD的度数,判断BE与AD是何种位置关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知任意三角形ABC,
(1)如图1,过点C作DE∥AB,求证:∠DCA=∠A;
(2)如图1,求证:三角形ABC的三个内角(即∠A、∠B、∠ACB)之和等于180°;
(3)如图2,求证:∠AGF=∠AEF+∠F;
(4)如图3,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=150°,求∠F.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是一个无理数筛选器的工作流程图.
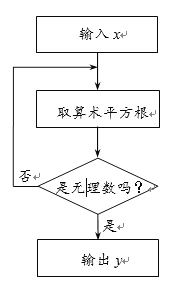
(1)当![]() 为16时,
为16时,![]() 值为 ;
值为 ;
(2)是否存在输入有意义的![]() 值后,却始终输不出
值后,却始终输不出![]() 值?如果存在,写出所有满足要求的
值?如果存在,写出所有满足要求的![]() 值;如果不存在,请说明理由;
值;如果不存在,请说明理由;
(3)如果输入![]() 值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的
值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的![]() 值可能是什么情况;
值可能是什么情况;
(4)当输出的![]() 值是
值是![]() 时,判断输入的
时,判断输入的![]() 值是否唯一,如果不唯一,请写出其中的两个.
值是否唯一,如果不唯一,请写出其中的两个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com