
 ��ͼ����ƽ��ֱ������ϵ�У�������y=$\frac{1}{2}$x2+bx+c����B��8��6������X�佻�ڵ�A��2��0������D���Գ�����x�ύ�ڵ�C���߶�BC���ӳ����������߽��ڵ�E������BD��DE��
��ͼ����ƽ��ֱ������ϵ�У�������y=$\frac{1}{2}$x2+bx+c����B��8��6������X�佻�ڵ�A��2��0������D���Գ�����x�ύ�ڵ�C���߶�BC���ӳ����������߽��ڵ�E������BD��DE������ ��1����B��8��6����A��2��0�����������߽���ʽ���ɽ�����⣮
��2����y=0���ⷽ�̼��ɵõ���D���꣬�����䷽������������꼴�ɣ�
��3�����ֱ��BC����ʽ�����÷����������E���꣬��S��BDE=S��CDE+S��CDB���ɽ�����⣮
��4�����P����Ϊ��m��$\frac{1}{2}$m2-4m+6�����г����̼��ɽ�����⣮
���  �⣺��1��������$\left\{\begin{array}{l}{32+8b+c=6}\\{2+2b+c=0}\end{array}\right.$��
�⣺��1��������$\left\{\begin{array}{l}{32+8b+c=6}\\{2+2b+c=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=-4}\\{c=6}\end{array}\right.$��
��2����y=$\frac{1}{2}$x2-4x+6=$\frac{1}{2}$��x-4��2-2��
�������߶�������Ϊ��4��-2����
��y=0����$\frac{1}{2}$x2-4x+6=0�����x=2��6��
���D������6��0����
��3����ֱ��BC����ʽΪy=kx+b������$\left\{\begin{array}{l}{4k+b=0}\\{8k+b=6}\end{array}\right.$
���$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=-6}\end{array}\right.$��
��ֱ��BC����ʽΪy=$\frac{3}{2}$x-6��
��$\left\{\begin{array}{l}{y=\frac{3}{2}x-6}\\{y=\frac{1}{2}{x}^{2}-4x+6}\end{array}\right.$���$\left\{\begin{array}{l}{x=8}\\{y=6}\end{array}\right.$��$\left\{\begin{array}{l}{x=3}\\{y=-\frac{3}{2}}\end{array}\right.$��
���E������3��-$\frac{3}{2}$����
��S��BDE=S��CDE+S��CDB=$\frac{1}{2}$��2��$\frac{3}{2}$+$\frac{1}{2}$��2��6=$\frac{15}{2}$��
��4�����P������m��$\frac{1}{2}$m2-4m+6����
������$\frac{1}{2}$��4��|$\frac{1}{2}$m2-4m+6|=$\frac{1}{4}$��$\frac{1}{2}$��2��6��
��$\frac{1}{2}$m2-4m+6=$��\frac{3}{4}$��
���m=$\frac{8��\sqrt{22}}{2}$��m=$\frac{8��\sqrt{10}}{2}$��
���P������$\frac{8+\sqrt{22}}{2}$��$\frac{3}{4}$����$\frac{8-\sqrt{22}}{2}$��$\frac{3}{4}$����$\frac{8+\sqrt{10}}{2}$��-$\frac{3}{4}$����$\frac{8-\sqrt{10}}{2}$��-$\frac{3}{4}$����
���� ���⿼����κ����ۺ��⡢����ϵ������һ�κ�����֪ʶ������Ĺؼ���������մ���ϵ������ѧ�����÷����������������������꣬ѧ��ת����˼��˼�����⣬������ת��Ϊ���̽���������п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��a��b��c�ǡ�ABC�����߳�����$\frac{a}{b}$=$\frac{a+b}{a+b+c}$��BD=c�����CAB����CBA�Ĺ�ϵ�ǣ�������
��ͼ��a��b��c�ǡ�ABC�����߳�����$\frac{a}{b}$=$\frac{a+b}{a+b+c}$��BD=c�����CAB����CBA�Ĺ�ϵ�ǣ�������| A�� | ��CAB��2��CBA | B�� | ��CBA=2��CAB | C�� | ��CAB��2��CBA | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����һ��P��ʹ�䵽A��B����ľ�����ȣ��ҵ���MON���ߵľ�����ȣ���ֻҪ������ͼ�ۼ���˵���������ĵ㣬����д����ͼ���̣�
����һ��P��ʹ�䵽A��B����ľ�����ȣ��ҵ���MON���ߵľ�����ȣ���ֻҪ������ͼ�ۼ���˵���������ĵ㣬����д����ͼ���̣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
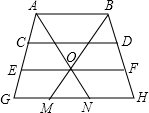 ��ͼ��AB��CD��EF��GH��AN��BM�Ľ���O��EF�ϣ���ͼ�����εĸ��������εĸ�����16��
��ͼ��AB��CD��EF��GH��AN��BM�Ľ���O��EF�ϣ���ͼ�����εĸ��������εĸ�����16���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��D�ǡ�ABC��BC����һ�㣬��B=��BAD����ADC=80�㣬��C=70�㣬���BAC=70�㣮
��ͼ��D�ǡ�ABC��BC����һ�㣬��B=��BAD����ADC=80�㣬��C=70�㣬���BAC=70�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{2}}{2}$ | C�� | $\frac{\sqrt{3}}{2}$ | D�� | $\frac{\sqrt{3}}{3}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com