练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．关于x的一元二次方程x2+（m-2）x-2m=0有两个相等的实数根，则m的值是（　　）
    A．-2B．2C．4+±$\sqrt{2}$D．0或8

    分析 由方程有两个相等的实数根结合根的判别式即可得出△=（m+2）2=0，解之即可得出结论．

    解答 解：∵关于x的一元二次方程x2+（m-2）x-2m=0有两个相等的实数根，
    ∴△=（m-2）2-4×1×（-2m）=m2+4m+4=（m+2）2=0，
    解得：m=-2．
    故选A．

    点评 本题考查了根的判别式，牢记“当△=0时，方程有两个相等的实数根”是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    16．某工厂甲、乙两名工人参加操作技能培训，现分别从他们在培训期间参加若干次测试成绩中随机抽取8次，计算得两人的平均成绩都是85分，方差分别是S甲2=35.5，S乙2=41，从操作技能稳定的角度考虑，选派甲参加比赛．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．观察下面三行数：
    -3，9，-27，81，-243，…
    -5，7，-29，79，-245，…
    -1，3，-9，27，-81，…
    （1）探索第一行数中的规律，并用含n的代数式表示第n个数：（-3）n；
    （2）第二、三行数与第一行数中相对应的数分别有什么关系？
    （3）分别取上边三行数中的第6个数，计算取出的三个数的和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．计算：-12012-[0.1252012×（-8）2013+（-12）÷6]2×$（-\frac{1}{5}）$+|-2|3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

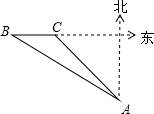    1．如图，海关缉私艇在A处接到情报，在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行，于是该艇立即沿北偏西45°的方向前进，经过1小时航行，恰好在C处截住可疑船只，则缉私艇的速度为（　　）
    A．（12$\sqrt{2}$+12$\sqrt{6}$）海里/时B．（12$\sqrt{3}$+12$\sqrt{6}$）海里/时C．（12$\sqrt{2}$+12$\sqrt{3}$）海里/时D．（8$\sqrt{3}$+8$\sqrt{6}$）海里/时

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．某班开展以“提倡勤俭节约，反对铺张浪费”为主题教育活动．为了解学生每天使用零花钱的情况，小明随机调查了10名同学，结果如下表：
    每天使用零花钱（单位：元）02345
    人数12412
    关于这10名同学每天使用的零花钱，下列说法正确的是（　　）
    A．A、平均数是3B．中位数是4C．众数是2D．方差是4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

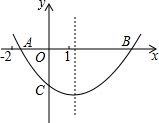    18．二次函数y=ax2+bx+c的图形如图，OA=OC，下列结论：①abc＜0；②4ac＜b2；③ac-b＜-1；④ac-2a+1＞0；⑤OB•OC=-$\frac{c}{a}$．其中结论正确的序号有（　　）
    A．②⑤B．②④⑤C．②③④⑤D．②③⑤

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图1，在平面直角坐标系中．直线y=-$\frac{1}{2}$x+3与x轴、y轴相交于A、B两点，动点C在线段OA上，将线段CB绕着点C顺时针旋转90°得到CD，此时点D恰好落在直线AB上时，过点D作DE⊥x轴于点E．
    （1）求证：△BOC≌△CED；
    （2）如图2，将△BCD沿x轴正方向平移得△B′C′D′，当直线B′C′经过点D时，求点D的坐标及△BCD平移的距离；
    （3）若点P在y轴上，点Q在直线AB上．是否存在以C、D、P、Q为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的Q点坐；若不存在，请说明理由．

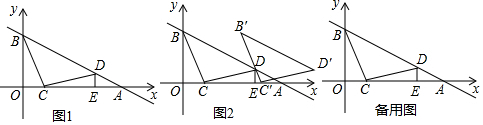
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．若代数式$\frac{x}{x+2}$在实数范围内有意义，则x的取值范为是（　　）
    A．x≥-2B．x≠2C．x≠0D．x≠-2

    查看答案和解析>>

    同步练习册答案